AP過去問令和7年度春期午後問3 プログラミング

AP過去問_令和7年度春期_午後_問4_システムアーキテクチャの同じ回の次の問題へ移動。

AP過去問_令和6年度秋期_午後_問3_プログラミングの前の回の同じカテゴリの問題へ移動。

令和7年度春期午後問3 プログラミング(AIプロンプト向け)

■スライドパズルを解くプログラムに関する次の記述を読んで、設問に答えよ。

　表1 のルールで定義されるスライドパズルについて考える。

<div><div class="table-container"><div class="table-header"><span class="table-title">表1 スライドパズルのルール</span><span class="table-unit"></span></div>

<tr>

</tr>

<tr>

<td align="center" style="border: 2px solid;">正方形の面に、1から順に1ずつ大きくなる数字の書かれた駒が配置されている。1か所だけ駒の置かれていない空白のマス(以下、空白マスという)がある。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">開始時点の盤面</td>

<td align="center" style="border: 2px solid;">開始時点では、駒と空白マスはランダムに配置されている。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">ゴールの盤面</td>

<td align="center" style="border: 2px solid;">盤面左上に数字が1の駒があり、右の駒の数字は1ずっ増えていき、その行の右端の駒に書かれた数字より1 大きい数字が、次の行の左端の駒の数字となる。盤面右下のマスが空白マスとなる。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">駒の上下左右いずれかに空白マスがある場合、駒を空白マスに移動することができる。駒が移動した場合、駒が置かれていたマスが空白マスになる。駒を空白マスに移動させて盤面を変化させ、ゴールの盤面と同じにすることを目指す。</td>

</tr>

</table>

</div>

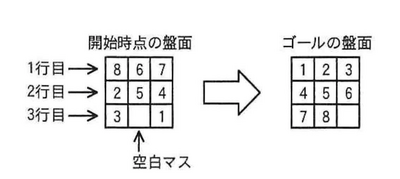
　―辺が3マスのスライドパズルの例を図1 に示す。

　図1 一辺が3マスのスライドパズルの例ここから

開始時点の盤面

縦方向に1行目、2行目、3行目

開始時点の盤面

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

　ゴールの盤面

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

　図1 一辺が3マスのスライドパズルの例ここまで

　本問では、ー辺のマスの個数が任意のスライドパズルにおいて、ゴールの盤面になるまでの駒の移動回数が最小となる移動方法(以下、最小解という)をーつ求めるプログラムを作成する。

〔一辺がNマスのスライドパズルの最小解をを用いて求る方法〕　幅優先探索を行ったときの、スライドパズルの盤面の遷移を、グラフで表現する。開始時点の盤面をルートノード、ある時点の盤面をノード、駒の移動に伴う盤面の遷移をエッジで表現する。また、ゴールの盤面をゴールノードとして定義する。

　幅優先探索で最小解を求める方法を次のように考える。ここで、Nは2以上とする。

　探索対象のノードに対して、移動できる駒ごとにその駒を移動した後のノードを作成して、探索対象のノードの子ノードとし、探索対象のノードは探索済みとなる。このとき、子ノードが表す盤面が既に探索したノード(以下、探索済みノードという)と同じであれば、この子ノードは終端ノードとして、以降の探索は行わない。また、子ノードがゴールノードと同じであれば、最小解が見つかったと判断して探索を終了する。

〔Nが3の場合の例〕

　ー辺が3マスのスライドパズルの最小解を求める過程の例を図2に示す。

　図2 一辺が3マスのスライドパズルの最小解を求める過程の例ここから

ルートノード

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

1回目としてルートノードの子ノード①～③がある。

子ノード①

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード②

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード③

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

2回目として子ノード①の子ノード④、⑤がある。2回目として子ノード②の子ノード⑥、⑦、⑧、⑨がある。2回目として子ノード③の子ノード⑩、⑪がある。⑤、⑥、⑩は終端ノード

子ノード④

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑤

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑥

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑦

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑧

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑨

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑩

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

子ノード⑪

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

以降の子ノードは省略。

n回目として、いづれかの子ノードの子ノード⑫をゴールノードとして

子ノード⑫

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

　図2 一辺が3マスのスライドパズルの最小解を求める過程の例ここまで

(1) 1回目の駒の移動では、ルートノードを探索対象のノードとする。ここでは、移動できる駒が三つあるので、ルートノードから深さが1となる①～③の子ノードを作成し、ルートノードは探索済みノードとなる。ここで、①～③の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。

(2) 次に、作成した子ノードで終端ノード以外のノードをそれぞれ探索対象のノードとし、駒の移動にあわせて子ノードを作成する。図2では、①～③のノードから④～⑪の子ノードを作成し、①～③は探索済みノードとなる。ここで、④～⑪の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。図2では、盤面が探索済みノードと一致する⑤、⑥及び⑩は終端ノードとなり、以降の探索は行わない。

(3) 以降、(2)で作成したノードの子ノードの作成と、ゴールノードの判定及び終端ノードの判定を繰り返す。図2の⑫は、n回目の移動でゴールノードに至ったことを示している。なお、全てのリーフノードが終端ノードと判定された場合、ゴールの盤面に至る駒の移動方法がないことを意味しているので、その旨のメッセージを出力して探索を終了する。

　次に、配列を用いた盤面の表現方法を図3に示す。ここで、空白マスを表す値は最も大きい駒の数字である8に1を加えた9とする。なお、配列の要素番号は1から始まるものとする。

　図3 配列を用いた盤面の表現方法ここから

盤面を次の例に示すように配列を用いて表現する。

(1) 盤面の行ごとに並ぶ駒の数字を整数型の配列で表す。

横方向に1列目、2列目、3列目

配列表現サンプル

<tr>

</tr>

<tr>

</tr>

<tr>

</tr>

</table>

1行目を表す配列 {8, 6, 7}、2行目を表す配列 {2, 5, 4}、3行目を表す配列 {3, 9, 1}

(2) (1)で行ごとに定義した配列を整数型配列の配列(以下、盤面配列という)で表す。

{{8, 6, 7}, {2, 5, 4}, {3, 9, 1}}

(3) 1行目の3列目の駒の数字は、盤面配列名をboardとするとboard[1][3]として参照する。

　図3 配列を用いた盤面の表現方法ここまで

〔ー辺がNマスのスライドパズルの最小解を求めるプログラム〕

　一辺がNマスのスライドパズルにおいて、開始時点の盤面をランダムに作成し、最小解を求め、開始時点の盤面からの遷移及び駒の移動回数を出力するプログラムを作成する。開始時点の盤面からの遷移を保持する単方向連結リストの要素となるクラスBoardStateの説明を図4に、キューを実現するクラスQueueの説明を図5に、リストを実現するクラスListの説明を図6に、プログラムで使用する主な関数を表2に、最小解を求めるプログラムを図7に示す。

<div><div class="table-container"><div class="table-header"><span class="table-title">図4 クラスBoardStateの説明</span><span class="table-unit"></span></div>

<tr>

<td align="center" style="border: 2px solid; width: 5em;">メンバ変数</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">board</td>

<td align="center" style="border: 2px solid;">整数型配列の配列</td>

<td align="center" style="border: 2px solid;">盤面配列。初期状態は未定義</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">space</td>

<td align="center" style="border: 2px solid;">整数型の配列</td>

<td align="center" style="border: 2px solid;">空白のマスの場所を示す行番号と列番号の二つの要素から成る配列。初期状態は未定義。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState</td>

<td align="center" style="border: 2px solid;">駒が1回移動する前のBoardStateのインスタンスへの参照。開始時点の盤面からの遷移を出力する際に用いる。初期状態は未定義。</td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">図4 クラスBoardStateの説明</span><span class="table-unit"></span></div>

<tr>

<td align="center" style="border: 2px solid; width: 5em;">コンストラクタ</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState()</td>

<td align="center" style="border: 2px solid;">インスタンスを初期化する。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState(BoardState: st)</td>

<td align="center" style="border: 2px solid;">インスタンスを初期化し、メンバ変数に次の処理を行う。</br> (1) メンバ変数boardに引数で渡されたBoardStateのインスタンスのboardの値を格納する。</br> (2) メンバ変数spaceに引数で渡されたBoardStateのインスタンスのspaceの値を格納する。</br> (3) メンバ変数prevに引数で渡されたBoardStateのインスタンスへの参照stを格納する。</br> </td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">図5 クラスQueueの説明</span><span class="table-unit"></span></div>

<tr>

<td align="center" style="border: 2px solid; width: 5em;">コンストラクタ</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">Queue()</td>

<td align="center" style="border: 2px solid;">可変長のキューを生成する。</td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">図5 クラスQueueの説明</span><span class="table-unit"></span></div>

<tr>

</tr>

<tr>

<td align="center" style="border: 2px solid;">add(BoardState: st)</td>

<td align="center" style="border: 2px solid;">キューにBoardStateのインスタンスへの参照stを追加する。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">isEmpty()</td>

<td align="center" style="border: 2px solid;">キューが空の場合はtrueを返し、空でない場合はfalseを返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState</td>

<td align="center" style="border: 2px solid;">先頭のBoardStateのインスタンスへの参照を取り出して返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState</td>

<td align="center" style="border: 2px solid;">先頭のBoardStateのインスタンスへの参照を返す。</td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">図6 クラスQueueの説明</span><span class="table-unit"></span></div>

<tr>

<td align="center" style="border: 2px solid; width: 5em;">コンストラクタ</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">可変長のリストを生成する。</td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">図6 クラスListの説明</span><span class="table-unit"></span></div>

<tr>

</tr>

<tr>

<td align="center" style="border: 2px solid;">add(整数型配列の配列: b)</td>

<td align="center" style="border: 2px solid;">リストに盤面配列bを追加する。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">isEmpty()</td>

<td align="center" style="border: 2px solid;">リストが空の場合はtrueを返し、空でない場合はfalseを返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">整数型配列の配列</td>

<td align="center" style="border: 2px solid;">リストの先頭に存在する盤面配列を返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">BoardState</td>

<td align="center" style="border: 2px solid;">先頭のBoardStateのインスタンスへの参照を返す。</td>

</tr>

</table>

</div>

<div><div class="table-container"><div class="table-header"><span class="table-title">表2 プログラムで使用する主な関数</span><span class="table-unit"></span></div>

<tr>

</tr>

<tr>

<td align="center" style="border: 2px solid;">createGoal(整数型: board_size)</td>

<td align="center" style="border: 2px solid;">整数型配列の配列</td>

<td align="center" style="border: 2px solid;">引数board_sizeの値を一辺のマス数としたスライドパズルのゴールの盤面を表す配列(以下、ゴールの盤面配列という)を作成して返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">createStart(整数型: board_size)</td>

<td align="center" style="border: 2px solid;">整数型配列の配列</td>

<td align="center" style="border: 2px solid;">引数board_sizeの値を一辺のマス数としたスライドパズルの開始時点の盤面配列をランダムに作成し、出力して返す。なお、ゴールの盤面配列と同じものが作成されることはない。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">getSpace(整数型配列の配列: b)</td>

<td align="center" style="border: 2px solid;">整数型の配列</td>

<td align="center" style="border: 2px solid;">盤面配列bを用いて、空白マスの場所と行番号と列番号から成る配列で返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">checkGoal(整数型配列の配列: b, 整数型配列の配列: g)</td>

<td align="center" style="border: 2px solid;">第一引数の盤面配列bと第二引数のゴールの盤面配列gを用いて両者が一致しているかどうかを判定して結果を返す。一致する場合はtrueを返し、一致しない場合はfalseを返す。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">printResult(BoardState: st)</td>

<td align="center" style="border: 2px solid;">引数として与えられたBoardStateのインスタンスへの参照stを用いて、開始時点の盤面からの遷移及び駒の移動回数を出力する。</td>

</tr>

<tr>

<td align="center" style="border: 2px solid;">checkSameBoard(整数型配列の配列: b, List: l)</td>

<td align="center" style="border: 2px solid;">引数で渡される探索済みの盤面配列のリストへの参照lを用いて、盤面配列bが探索済みの盤面配列のリストに存在するかどうかを判定して結果を返す。存在する場合はtrueを返し、存在しない場合はfalseを返す。</td>

</tr>

</table>

</div>

　図7 最小解を求めるプログラムここから

<style>

.line {

position: relative;

padding-left: 2.5em;

}

.line::before {

content: attr(data-line);

position: absolute;

left: 0;

width: 2em;

text-align: right;

user-select: none;

}

</style>

<span class="line" data-line="01:">〇solveNPuzzle(整数型: board_size)</span>

<span class="line" data-line="02:"> BoardState: start_state /* 開始時点の盤面を保持するBoardStateのインスタンスへの参照 */</span>

<span class="line" data-line="03:"> 整数型配列の配列: goal_board /* ゴールの盤面配列 */</span>

<span class="line" data-line="04:"> 整数型配列の配列: direction /* 駒の移動に伴う空白マスの移動方向を行番号の増減を1番目の要素、列番号の増減を2番目の要素で表現する配列 */</span>

<span class="line" data-line="05:"> Queue: explore_queue /* 探索対象の盤面を保持するキューのインスタンスへの参照 */</span>

<span class="line" data-line="06:"> List: check_list /* 探索済みの盤面配列を保持するリストのインスタンスへの参照 */</span>

<span class="line" data-line="07:"> BoardState: state /* 駒が移動する前の盤面を保持するBoardStateのインスタンスへの参照 */</span>

<span class="line" data-line="08:"> BoardState: new_state /* 駒が移動した後の盤面を保持するBoardStateのインスタンスへの参照 */</span>

<span class="line" data-line="09:"> 整数型: change_num /* 移動する駒の数字 */</span>

<span class="line" data-line="10:"> 整数型: i /* forループ内で使用するカウンタ変数 */</span>

<span class="line" data-line="11:"> start_state ← BoardState() </span>

<span class="line" data-line="12:"> goal_board ← createGoal(board_size) </span>

<span class="line" data-line="13:"> start_state.board ← createStart(board_size) </span>

<span class="line" data-line="14:"> start_state.space ← getSpace(start_state.board) </span>

<span class="line" data-line="15:"> direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}} </span>

<span class="line" data-line="16:"> explore_queue ← Queue() </span>

<span class="line" data-line="17:"> explore_queue.add(start_state) </span>

<span class="line" data-line="18:"> check_list ← List() </span>

<span class="line" data-line="19:"> check_list.add(start_state.board) </span>

<span class="line" data-line="20:"> while(【ア】がfalseと等しい) </span>

<span class="line" data-line="21:"> state ← explore_queue.【イ】</span>

<span class="line" data-line="22:"> for(iを1からdirectionの要素数まで1ずつ増やす) </span>

<span class="line" data-line="23:"> if((state.space[1] +【ウ】が1以上) かつ </span>

<span class="line" data-line="24:"> (state.space[1] +【ウ】が【エ】以下) かつ </span>

<span class="line" data-line="25:"> (state.space[2] +【オ】が1以上) かつ </span>

<span class="line" data-line="26:"> (state.space[2] +【オ】が【エ】以下)) </span>

<span class="line" data-line="27:"> new_state ← BoardState(state) </span>

<span class="line" data-line="28:"> new_state.space[1] ← state.space[1] + 【ウ】</span>

<span class="line" data-line="29:"> new_state.space[2] ← state.space[2] + 【オ】</span>

<span class="line" data-line="30:"> change_num ← new_state.board[new_state.space[1]][new_state.space[2]]</span>

<span class="line" data-line="31:"> new_state.board[new_state.space[1]][new_state.space[2]] ← board_size * board_size </span>

<span class="line" data-line="32:"> new_state.boart[state.space[1]][state.space[2]] ← change_num </span>

<span class="line" data-line="33:"> if(【カ】がtrueと等しい) </span>

<span class="line" data-line="34:"> printResult(new_state) </span>

<span class="line" data-line="35:"> return </span>

<span class="line" data-line="36:"> endif </span>

<span class="line" data-line="37:"> if(checkSameBoard(new_state.board, check_list)がfalseと等しい) </span>

<span class="line" data-line="38:"> explore_queue.【キ】 </span>

<span class="line" data-line="39:"> check_list.【ク】 </span>

<span class="line" data-line="40:"> endif </span>

<span class="line" data-line="41:"> endif </span>

<span class="line" data-line="42:"> endfor </span>

<span class="line" data-line="43:"> endwhile </span>

<span class="line" data-line="44:"> ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力 </span>

<span class="line" data-line="45:"> return </span>

</code></pre>

　図7 最小解を求めるプログラムここまで

設問1　図2中の②の盤面を図3に倣って、配列で答えよ。

設問2　図7中の【ア】～【ク】に入れる適切な字句を答えよ。

令和7年度春期午後問3 プログラミング(問題原文)

■スライドパズルを解くプログラムに関する次の記述を読んで、設問に答えよ。

　表1 のルールで定義されるスライドパズルについて考える。

表1 スライドパズルのルール

用語	説明
盤面	正方形の面に、1から順に1ずつ大きくなる数字の書かれた駒が配置されている。1か所だけ駒の置かれていない空白のマス(以下、空白マスという)がある。
開始時点の盤面	開始時点では、駒と空白マスはランダムに配置されている。
ゴールの盤面	盤面左上に数字が1の駒があり、右の駒の数字は1ずっ増えていき、その行の右端の駒に書かれた数字より1 大きい数字が、次の行の左端の駒の数字となる。盤面右下のマスが空白マスとなる。
駒の移動	駒の上下左右いずれかに空白マスがある場合、駒を空白マスに移動することができる。駒が移動した場合、駒が置かれていたマスが空白マスになる。駒を空白マスに移動させて盤面を変化させ、ゴールの盤面と同じにすることを目指す。

　―辺が3マスのスライドパズルの例を図1 に示す。

　図1 一辺が3マスのスライドパズルの例

　本問では、ー辺のマスの個数が任意のスライドパズルにおいて、ゴールの盤面になるまでの駒の移動回数が最小となる移動方法(以下、最小解という)をーつ求めるプログラムを作成する。

〔一辺がNマスのスライドパズルの最小解をを用いて求る方法〕　幅優先探索を行ったときの、スライドパズルの盤面の遷移を、グラフで表現する。開始時点の盤面をルートノード、ある時点の盤面をノード、駒の移動に伴う盤面の遷移をエッジで表現する。また、ゴールの盤面をゴールノードとして定義する。

　幅優先探索で最小解を求める方法を次のように考える。ここで、Nは2以上とする。

　探索対象のノードに対して、移動できる駒ごとにその駒を移動した後のノードを作成して、探索対象のノードの子ノードとし、探索対象のノードは探索済みとなる。このとき、子ノードが表す盤面が既に探索したノード(以下、探索済みノードという)と同じであれば、この子ノードは終端ノードとして、以降の探索は行わない。また、子ノードがゴールノードと同じであれば、最小解が見つかったと判断して探索を終了する。

〔Nが3の場合の例〕

　ー辺が3マスのスライドパズルの最小解を求める過程の例を図2に示す。

　図2 一辺が3マスのスライドパズルの最小解を求める過程の例

(1) 1回目の駒の移動では、ルートノードを探索対象のノードとする。ここでは、移動できる駒が三つあるので、ルートノードから深さが1となる①～③の子ノードを作成し、ルートノードは探索済みノードとなる。ここで、①～③の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。

(2) 次に、作成した子ノードで終端ノード以外のノードをそれぞれ探索対象のノードとし、駒の移動にあわせて子ノードを作成する。図2では、①～③のノードから④～⑪の子ノードを作成し、①～③は探索済みノードとなる。ここで、④～⑪の子ノードに対して、ゴールノードの判定及び終端ノードの判定を行う。図2では、盤面が探索済みノードと一致する⑤、⑥及び⑩は終端ノードとなり、以降の探索は行わない。

(3) 以降、(2)で作成したノードの子ノードの作成と、ゴールノードの判定及び終端ノードの判定を繰り返す。図2の⑫は、n回目の移動でゴールノードに至ったことを示している。なお、全てのリーフノードが終端ノードと判定された場合、ゴールの盤面に至る駒の移動方法がないことを意味しているので、その旨のメッセージを出力して探索を終了する。

　次に、配列を用いた盤面の表現方法を図3に示す。ここで、空白マスを表す値は最も大きい駒の数字である8に1を加えた9とする。なお、配列の要素番号は1から始まるものとする。

　図3 配列を用いた盤面の表現方法ここまで

〔ー辺がNマスのスライドパズルの最小解を求めるプログラム〕

　一辺がNマスのスライドパズルにおいて、開始時点の盤面をランダムに作成し、最小解を求め、開始時点の盤面からの遷移及び駒の移動回数を出力するプログラムを作成する。開始時点の盤面からの遷移を保持する単方向連結リストの要素となるクラスBoardStateの説明を図4に、キューを実現するクラスQueueの説明を図5に、リストを実現するクラスListの説明を図6に、プログラムで使用する主な関数を表2に、最小解を求めるプログラムを図7に示す。

メンバ変数	型	説明
board	整数型配列の配列	盤面配列。初期状態は未定義
space	整数型の配列	空白のマスの場所を示す行番号と列番号の二つの要素から成る配列。初期状態は未定義。
prev	BoardState	駒が1回移動する前のBoardStateのインスタンスへの参照。開始時点の盤面からの遷移を出力する際に用いる。初期状態は未定義。

コンストラクタ	説明
BoardState()	インスタンスを初期化する。
BoardState(BoardState: st)	インスタンスを初期化し、メンバ変数に次の処理を行う。 (1) メンバ変数boardに引数で渡されたBoardStateのインスタンスのboardの値を格納する。 (2) メンバ変数spaceに引数で渡されたBoardStateのインスタンスのspaceの値を格納する。 (3) メンバ変数prevに引数で渡されたBoardStateのインスタンスへの参照stを格納する。

図4 クラスBoardStateの説明

コンストラクタ	説明
Queue()	可変長のキューを生成する。

メソッド	戻り値	説明
add(BoardState: st)	なし	キューにBoardStateのインスタンスへの参照stを追加する。
isEmpty()	論理型	キューが空の場合はtrueを返し、空でない場合はfalseを返す。
poll()	BoardState	先頭のBoardStateのインスタンスへの参照を取り出して返す。
peek()	BoardState	先頭のBoardStateのインスタンスへの参照を返す。

図5 クラスQueueの説明

コンストラクタ	説明
List()	可変長のリストを生成する。

メソッド	戻り値	説明
add(整数型配列の配列: b)	なし	リストに盤面配列bを追加する。
isEmpty()	論理型	リストが空の場合はtrueを返し、空でない場合はfalseを返す。
peek()	整数型配列の配列	リストの先頭に存在する盤面配列を返す。

図6 クラスListの説明

表2 プログラムで使用する主な関数

名称	戻り値	説明
createGoal(整数型: board_size)	整数型配列の配列	引数board_sizeの値を一辺のマス数としたスライドパズルのゴールの盤面を表す配列(以下、ゴールの盤面配列という)を作成して返す。
createStart(整数型: board_size)	整数型配列の配列	引数board_sizeの値を一辺のマス数としたスライドパズルの開始時点の盤面配列をランダムに作成し、出力して返す。なお、ゴールの盤面配列と同じものが作成されることはない。
getSpace(整数型配列の配列: b)	整数型の配列	盤面配列bを用いて、空白マスの場所と行番号と列番号から成る配列で返す。
checkGoal(整数型配列の配列: b, 整数型配列の配列: g)	論理型	第一引数の盤面配列bと第二引数のゴールの盤面配列gを用いて両者が一致しているかどうかを判定して結果を返す。一致する場合はtrueを返し、一致しない場合はfalseを返す。
printResult(BoardState: st)	なし	引数として与えられたBoardStateのインスタンスへの参照stを用いて、開始時点の盤面からの遷移及び駒の移動回数を出力する。
checkSameBoard(整数型配列の配列: b, List: l)	論理型	引数で渡される探索済みの盤面配列のリストへの参照lを用いて、盤面配列bが探索済みの盤面配列のリストに存在するかどうかを判定して結果を返す。存在する場合はtrueを返し、存在しない場合はfalseを返す。


〇solveNPuzzle(整数型: board_size)
 BoardState: start_state /* 開始時点の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型配列の配列: goal_board /* ゴールの盤面配列 */
 整数型配列の配列: direction /* 駒の移動に伴う空白マスの移動方向を行番号の増減を1番目の要素、列番号の増減を2番目の要素で表現する配列 */
 Queue: explore_queue /* 探索対象の盤面を保持するキューのインスタンスへの参照 */
 List: check_list /* 探索済みの盤面配列を保持するリストのインスタンスへの参照 */
 BoardState: state /* 駒が移動する前の盤面を保持するBoardStateのインスタンスへの参照 */
 BoardState: new_state /* 駒が移動した後の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型: change_num /* 移動する駒の数字 */
 整数型: i /* forループ内で使用するカウンタ変数 */
 start_state ← BoardState() 
 goal_board ← createGoal(board_size) 
 start_state.board ← createStart(board_size) 
 start_state.space ← getSpace(start_state.board) 
 direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}} 
 explore_queue ← Queue() 
 explore_queue.add(start_state) 
 check_list ← List() 
 check_list.add(start_state.board) 
 while(【 ア 】がfalseと等しい) 
   state ← explore_queue.【 イ 】
   for(iを1からdirectionの要素数まで1ずつ増やす) 
     if((state.space[1] +【 ウ 】が1以上) かつ 
        (state.space[1] +【 ウ 】が【 エ 】以下) かつ 
        (state.space[2] +【 オ 】が1以上) かつ 
        (state.space[2] +【 オ 】が【 エ 】以下)) 
       new_state ← BoardState(state) 
       new_state.space[1] ← state.space[1] + 【 ウ 】
       new_state.space[2] ← state.space[2] + 【 オ 】
       change_num ← new_state.board[new_state.space[1]][new_state.space[2]]
       new_state.board[new_state.space[1]][new_state.space[2]] ← board_size * board_size 
       new_state.boart[state.space[1]][state.space[2]] ← change_num 
       if(【 カ 】がtrueと等しい) 
         printResult(new_state) 
         return 
       endif 
       if(checkSameBoard(new_state.board, check_list)がfalseと等しい) 
         explore_queue.【 キ 】 
         check_list.【 ク 】 
       endif 
     endif 
   endfor 
 endwhile 
 ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力 
 return

図7 最小解を求めるプログラム

設問1　図2中の②の盤面を図3に倣って、配列で答えよ。

設問2　図7中の【ア】～【ク】に入れる適切な字句を答えよ。

回答・解説

　この問題…。みた瞬間危険な香りのするプログラミングです。ゲームプログラミングを知らない素人には危険すぎる幅優先探索という意味の分からない探索名。結局、全つぶしゲーなんだけど、そのすさまじい構想についていけないものにとっては未知なるプログラミングです。

　スライドパズル。あー子供のころやったやった。みたいな中年のおじさんのなんと多いことか…。アナログの奴。今の子供たちは経験しているのだろうか…。正直、あれに攻略法があるとか考えたことなかった。

　なるほどなー。問題を読んでるとそんなふうにスライドパズルは解けるのか。関心するわー。とか思いましたが、管理人はこの問題、手ごわすぎて、プライドを捨てるように、プログラムの問題を捨てました。これなら問11の勤務管理システムの問題の方がわかりやすいという微妙な判断に至ります。でも、試験の終わった今、もう一度、逃げないで考えてみようと思います。

　簡単に日本語で説明するなら、初期条件に与えられたパズルから動かし得る、すべての動かし方を試していく。うごかしたら、すでに見たことのある盤面として記録して、まったく同じ盤面になったら、そこから先はこれまでの探索に戻るから、その探索は終了。未知の盤面を全てやっていくという手順です。そのとき、どの動かし方を優先して試すのかというのを問題文で読み解かなければならないよっていう問題です。

　ってこのように前置きして説明してくれていたら、この問題を解く気になったかもしれない。初見で、何をやろうとしてるか。さっぱりわからないところから、たった30分で読み解くのは無理ゲーすぎる。危険な挑戦だわ。この問題。過去。最強の鬼畜ゲームの開発だわ。やばすぎる。この問題を選択した時点で技術者失格なんじゃないかと思うくらいリスクの高い開発。30分でできなければ死亡よ。という開発に挑む会社の方針があったとしたら怖すぎる。危険すぎる。そんな感じだね。

設問1

　動かせる全ての方法を試していくという方針のもとで行くと、初期値が下段中央に空白マスがあるので、①は下段左の３を空白マスに、③は下段右の１を空白マスに移動しています。そうすると、②は中央の５を空白マスに移動した形になります。なので、図3で説明されている配列の表現であらわすだけです。

したがって

{{8, 6, 7}, {2, 9, 4}, {3, 5, 1}}

が答えです。

　真ん中が空白になったあと、⑥は空白マスの下の５と交換して、ルートノードと同じ盤面になって、終端ノードになりますね。⑦は空白マスと左の２と交換してます。⑧は空白マスの上の６と交換してます。⑨は空白マスの右の４と交換してます。なので、この下、左、上、右の順番ってのは関係してきそうだなって覚えときましょか。違ったらすんません。

設問2

　1行目～19行目は各変数の初期化や関数を使っての初期化の類の処理をしています。10行目までは問題文でコメントとしても記載されるような初期化です。

11行目～19行目までの処理を確認しておきましょう。

11行目: start_state ← BoardState()

　BoardState型のstart_state変数をBoardState()コンストラクタを呼び出して初期化しています。

　start_stateクラス変数は以下のメンバ変数を保持しています

　・start_state.board:整数型配列の配列(盤面配列を保持できるメンバ変数)

　・start_state.space:整数型配列の配列(空白マスの行番号と列番号)

　・start_state.prev:BoardStateクラスのインスタンスへの参照(駒が1回移動する前の盤面状態クラスを保持するため)

　まだ各メンバ変数は何も保持していない。

12行目: goal_board ← createGoal(board_size)

　整数型配列の配列 goal_boardにboard_size(ここでは仮にboard_sizeは3として考えましょう。)に対応するゴール盤面の整数型配列の配列を設定しています。board_size=3なら具体的には{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}が返されます。これがゴールです。こんな試験の問題ならboard_sizeは3で固定の問題でもいいような気がするけど。いろいろな値でも動くし、任意の値にしとくかみたいな感じ。

13行目: start_state.board ← createStart(board_size)

　start_stateクラス変数のメンバ変数boardにboard_sizeに対応するスタート時の値をランダムに整数型配列の配列を設定します。ここでは問題文にあるとおりの初期状態が設定されるものとして考えましょう。具体的には{{8, 6, 7}, {2, 5, 4}, {3, 9, 1}}が返されます。

14行目: start_state.space ← getSpace(start_state.board)

　start_stateクラス変数のメンバ変数spaceにスタート時の盤面の空白マス9がある行番号, 列番号の配列を返します。問題文のとおりの例では具体的には{2, 3}という整数型の配列の値が返されます。

15行目: direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}}

　空白マスを移動させる方向の相対座標が格納された整数型配列の配列値を取得します。問題文と同じ順番で確認するようになっているようです。念のため確認しておきましょう。

　・最初の要素は{1, 0}なので列は固定で、行は一つ増えて下方向交換ですね。

　・最初の要素は{0, -1}なので行は固定で、列は一つ減って左方向交換ですね。

　・最初の要素は{-1, 0}なので列は固定で、行は一つ減って上方向交換ですね。

　・最初の要素は{0, 1}なので行は固定で、列は一つ増えて右方向交換ですね。

　下・左・上・右。覚えておいた順番ですね。よしよし。

16行目: explore_queue ← Queue()

　Queueクラス型の変数explore_queueに可変長のキューを生成するコンストラクタを実行した値で初期化する。実体化ですね。特にメンバ変数があるわけでもないですが、実体化されて、各メソッド関数が使えるようになりました。

　explore_queueクラス変数は以下のメソッドを保持しています

　・explore_queue.add(BoardState: st) BoardState型の引数を受け取りキューにstの参照を追加する関数。

　・explore_queue.isEmpty() キューが空ならtrue、空でないならfalseを返す関数。

　・explore_queue.poll() キューの先頭の参照を取り出して、取り出したBoardState型のクラス変数の参照を返す関数。

　・explore_queue.peek() キューの先頭のBoardState型のクラス変数の参照を返す関数。

17行目: explore_queue.add(start_state)

　早速、キューに初期化で作ったstart_stateクラス変数への参照を追加しました。

18行目: check_list ← List()

　Listクラス型の変数check_listに可変長のリストを生成するコンストラクタを実行した値で初期化する。実体化ですね。特にメンバ変数があるわけでもないですが、実体化されて、各メソッド関数が使えるようになりました。

　check_listクラス変数は以下のメソッドを保持しています。

　・check_list.add(整数型配列の配列: b) 整数型配列の配列の引数を受け取りリストに追加する関数。

　・check_list.isEmpty() リストが空ならtrue、空でないならfalseを返す関数。

　・check_list.peek() リストの先頭の整数型配列の配列を返す関数。

19行目: check_list.add(start_state.board)

　早速、リストに初期化で作ったstart_state.boardの整数型配列の配列を追加しました。

　リストは盤面の状態の古いものを奥に押し込んでいくクラスで、キューは状態クラスの古いものを奥に押し込んでいくクラスになっていますね。

　ここまでで、2行目～9行目で準備したのに使わなかった初期値として、

　BoardStateクラス型のstateとnew_state。

　整数型のchange_numとi

　以上の4変数はまだ使われていません。このあと使っていくことになるので、気に留めておきましょう。

　さて、さっそく20行目に穴埋めが来ます。アがfalseの間はまだまだややこしい問題を解くための処理が待っていて、アがtrueになると、もう問題を解く必要がなく、ゴールには至らないことが判明して終了する処理になっています。

　checkGoal関数だと、trueのときは解が見つかったことになります。falseのときは解はみつかっていないので、処理が続けられそうですが、解が見つかってtrueになったのに44行目でゴールの盤面に至る駒の移動方法がない旨のメッセージを出力とあるので、これでは具合が悪いので、こういうことではなさそうです。

　そうするとQueueクラスやListクラスで参照されているものが無くなったときと考えることもできますが、Listクラスには、addしたものを取り出すという概念はありません。詰め込んでいくだけの機能です。どこかでexplore_queur.add(なにがし)とexplore_queur.poll()のような関数を実行して、動かすべき盤面を増やしたり減らしたりして管理し、空白マスを動かして確認する作業をひとつづつ確認して、すすめていく、動かすべき盤面は最小で角のときの2方向、最大で4方向になり、確かめるべき盤面は2個～4個増えて、1つづつ取り出していき、それが無くなったら動かす盤面がもうないということなので、処理終了という感じに出来るのでは？という想像力が働かないと、ここを突破することはできません。

　しかも、ここで言ったexplore_queue.addもexplore_queue.poll()も問題文のプログラムの中にはありませんので、両方とも穴埋めになってるのだなと感づかないといけないっていう。想像力の塊でないと気づけないあたりです。想像力豊かな人は穴埋めのイとキのどっちかがどっちかなんだろうなまで、想像できてしまうわけです。

　ここまでくるとQueue型のexplore_queueとList型のcheck_listの変数の使い方もほぼ明確になってきているのがプログラマですよね。explore_queueは空白マスの入れ替えて、同じ盤面あって、それ以上探索する必要のなくなったものを取り出すというような処理をして、List型のcheck_listは過去の盤面を覚えるためにどんどん盤面を蓄えていくための変数だということに気づきます。

　すげぇぜ想像力。穴埋めのプログラムで何をしようとしているか、全貌をつかむ想像力が必要な問題です。

　ちょっと眺めると33行目から36行目のifブロックではprintResult関数があって結果を出力しようとしているので解が見つかった時の処理をしているなぁ。するとカはcheckGoal関数を使った条件式なのかなという想像力。

　そして、37行目から40行目のifブロックでは、同じ盤面はなかったときの処理をしている。このときQueueとListの変数になにか操作しているけど、これは、確かめなくてはいけない盤面の追加の処理をやっているんだろうなという想像力が働きます。

　そうすると、21行目は盤面の確認の消費側の処理かなという想像もできます。

　さらには23行目から26行目のif文は行列の空白マスが1以上、盤面の大きさ以内にある間の処理であったり、28行目29行目ではif文の条件式と同じ値を使って、空白マスにするべき行列の計算をしてそうだなという想像力。

　さらには30行目から32行目で盤面の空白マスと数字のマスの交換をしているということが想像できるわけです。

　ここまで想像できてやっとスタートラインに立てる問題です。

　というわけで探索するものがもうないかどうかを確かめる20行目のアは

したがって

ア　explore_queue.isEmpty()

が答えです。

　ですね。もちろん最初の1回目の判定はfalseになるのでwhileのループに突入しますし、もしGoalにたどり着くことなく、探索するものがなくなったら、ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力でいいわけですね。

　そして、すぐにまた穴埋めです。stateには、これから次の空白マス交換作業をする盤面の状態を取得します。stateにexplore_queueの中身を取り出すと空になってisEmpty()の結果がfalseになってしまいますが、すぐにexplore_queueの中身は補充されます。state ← explore_queue.poll()です。

したがって

イ　poll()

が答えです。

　次は穴埋めじゃないので助かりました。読み解くだけです。for文でiを1～4(directionの要素数)までで繰り返すというものです。この狙いは行方向のdirection[i][1]と列方向のdirection[i][2]を使うために1ずつ変化する変数iを活用するというところにあると考えてよいです。

　direction={{1, 0}, {0, -1}, {-1, 0}, {0, 1}}で

下方向交換: direction[1][1]=1、direction[1][2]=0

左方向交換: direction[2][1]=0、direction[2][2]=-1

上方向交換: direction[3][1]=-1、direction[3][2]=0

右方向交換: direction[4][1]=0、direction[4][2]=1

　ここまで、心構えした上でなら23行目～26行目のif文は簡単に答えれるでしょう。

(state.space[1] +【ウ】が1以上)かつ(state.space[1] +【ウ】が【エ】以下)かつ(state.space[2] +【オ】が1以上)かつ(state.space[2] +【オ】が【エ】以下)

　問題文の例で初期値を扱っているので、最初は一番下の行の真ん中の列が空白マスで{3, 2}がstate.spaceの配列値で

　state.space[1]にはこれから処理する盤面の空白マスの行番号情報の3が格納されています。

　state.space[2]にはこれから処理する盤面の空白マスの列番号情報が2が格納されています。

　現在の盤面の空白マスの位置に対してdirectionの要素を足し合わせた次の空白マスの位置が盤面の内側に存在しているかをチェックしています。行番号が1以上3以下、列番号が1以上3以下になっているかを確認するためのif文です。空白マスの移動後、盤面の内側に存在しなくなるパターンについては探索する必要がないので、このif文によるチェックが必要です。3以下になっているかをチェックするには、便宜上、問題文の例の3を採用していましたが、3という数字は実際にはboard_sizeという変数に格納されています。先にエから解決できますね。

したがって、

エ　board_size

が答えです。

(state.space[1] +【ウ】が1以上)かつ(state.space[1] +【ウ】が board_size 以下)かつ(state.space[2] +【オ】が1以上)かつ(state.space[2] +【オ】が board_size 以下)

ウはi番目のdirectionの行方向の要素を指定して、オはi番目のdirectionの列方向の要素を指定します。

したがって

ウ　direction[i][1]

オ　direction[i][2]

が答えです。

　ここまで来ると穴埋めはあと3つしかありません。プログラムの主要な部分の動きが見えてきましたね。一回ここで、ここまでの穴埋め解答を埋めたプログラムを表示しておきます。


〇solveNPuzzle(整数型: board_size)
 BoardState: start_state /* 開始時点の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型配列の配列: goal_board /* ゴールの盤面配列 */
 整数型配列の配列: direction /* 駒の移動に伴う空白マスの移動方向を行番号の増減を1番目の要素、列番号の増減を2番目の要素で表現する配列 */
 Queue: explore_queue /* 探索対象の盤面を保持するキューのインスタンスへの参照 */
 List: check_list /* 探索済みの盤面配列を保持するリストのインスタンスへの参照 */
 BoardState: state /* 駒が移動する前の盤面を保持するBoardStateのインスタンスへの参照 */
 BoardState: new_state /* 駒が移動した後の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型: change_num /* 移動する駒の数字 */
 整数型: i /* forループ内で使用するカウンタ変数 */
 start_state ← BoardState() 
 goal_board ← createGoal(board_size) 
 start_state.board ← createStart(board_size) 
 start_state.space ← getSpace(start_state.board) 
 direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}} 
 explore_queue ← Queue() 
 explore_queue.add(start_state) 
 check_list ← List() 
 check_list.add(start_state.board) 
 while(explore_queue.isEmpty()がfalseと等しい) 
   state ← explore_queue.poll()
   for(iを1からdirectionの要素数まで1ずつ増やす) 
     if((state.space[1] + direction[i][1] が1以上) かつ 
        (state.space[1] + direction[i][1] が board_size 以下) かつ 
        (state.space[2] + direction[i][2] が1以上) かつ 
        (state.space[2] + direction[i][2] が board_size 以下)) 
       new_state ← BoardState(state) 
       new_state.space[1] ← state.space[1] + direction[i][1]
       new_state.space[2] ← state.space[2] + direction[i][2]
       change_num ← new_state.board[new_state.space[1]][new_state.space[2]]
       new_state.board[new_state.space[1]][new_state.space[2]] ← board_size * board_size 
       new_state.boart[state.space[1]][state.space[2]] ← change_num 
       if(【 カ 】がtrueと等しい) 
         printResult(new_state) 
         return 
       endif 
       if(checkSameBoard(new_state.board, check_list)がfalseと等しい) 
         explore_queue.【 キ 】 
         check_list.【 ク 】 
       endif 
     endif 
   endfor 
 endwhile 
 ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力 
 return

27行目: new_state ← BoardState(state)

　新しい空白マス移動後の盤面を作っていきます。現在の盤面stateは残しておいて、new_stateという変数にBoardState(state)としてstateの内容をコピーしたような初期値として生成した参照を代入しています。

　new_stateクラス変数は以下のメンバ変数を保持しています

　・new_state.board:整数型配列の配列(盤面配列を保持できるメンバ変数 state.board)

　・new_state.space:整数型配列の配列(空白マスの行番号と列番号 state.space)

　・new_state.prev:BoardStateクラスのインスタンスへの参照(state)

　のように現在の盤面の情報がそれぞれのメンバ変数に設定されます。メンバ変数.prevには現在の盤面のBoardStateクラスの実体への参照を格納している点は注意しておきたいところです。

28行目: new_state.space[1] ← state.space[1] + direction[i][1]

　新しい盤面に次の空白マス交換をしたときの空白マス情報設定します。最下段の中央にあった空白マスに対して、下方向交換の処理は行番号4との交換となってしまうので、if文の条件判定で除外され、次に左方向交換の処理として27行目28行目の処理がしかかります。するとstate.space[1]は3でdirection[2][1]は0でnew_state.space[1]は3です。つまり変化しません。同じ行での操作なのであってますね。次の29行目では真ん中から左に空白マスが移動する演算がされますので、それを確認しましょう。

29行目: new_state.space[2] ← state.space[2] + direction[i][2]

　state.space[2]は2でdirection[2][2]は-1でnew_state.space[1]は1です。つまり、空白マスは一番左の列に移動した状態になります。あとは、new_state.boardの2次元配列でnew_state.boardのnew_state.spaceの座標の行列番号の値を、変換用の一時変数に取り出して、new_state.boardの2次元配列でnew_state.boardのnew_state.spaceの座標の行列番号に空白マスの値を入れて、 new_state.boardの2次元配列でstate.boardのstate.spaceの座標(元の空白マスの座標)の行列番号に一時的に記憶させた変数の値を格納すればいいって感じですね。それが30行目から32行目でやっていることです。

30行目: change_num ← new_state.board[new_state.space[1]][new_state.space[2]]

　新しい盤面の新しい空白マスの座標の位置に入ってる値は、問題の例なら3が入ってる。これをchange_numにとっておく。

31行目: new_state.board[new_state.space[1]][new_state.space[2]] ← board_size * board_size

　空白マスを意味する値はboard_size * board_sizeですね。board_sizeが3の場合は9ですもんね。合ってますね。他の方法でもやれますよね。state.board[state.board.space[1]][state.board.space[2]]から取得してもいいんだよね。まぁでも、board_size * board_sizeっていうのは冴えてる人のやり方にも感じる。

　新しい盤面の新しい空白マスの座標の位置に、9を設定。

32行目: new_state.boart[state.space[1]][state.space[2]] ← change_num

　新しい盤面の元の空白マスの座標の位置に、3を設定。という感じの処理。という感じで、元の盤面から考えられ新しい盤面を作ります。これをQueueクラスのexplore_queue登録するのとListクラスに登録しないとだめですね。

　じゃ、次の穴埋め33行目を考えましょう。

　前におおまかな流れを考えた時のとおり、このif文ブロックで条件が成立したときはprintResult(new_state)で、new_state.prevの情報をたどっていけば、正解の経路を表示することができて、印刷処理ができます。つまり、新しい盤面がゴールと一致したかをこのif文でチェックしています。checkGoal関数はゴールと思われる盤面(つまりnew_state)の整数型配列の配列(new_state.board)を引数に設定することになっています。それと最初に準備したゴールの盤面の整数型配列の配列goal_boardを第二引数に設定します。

したがって、

カ　checkGoal(new_state.board, goal_board)

が答えです。

34行目: printResult(new_state)

　結果を印刷する関数です。どんな結果表示をしてくれるのかは謎のままですが、プログラムでは、その先を知らないでプログラミングをするというのが真骨頂です。こういう、結果表示をしらないまま、間のプログラミングをするということになれていかないといけないと思います。歯車としてのプログラマはね。一人で全部作っちゃう系の方が面白いのはやっぱり中身も結果も見たい！っていう人だね。

35行目: return

　処理終了です。この関数から抜け出します。

36行目: endif

　ifブロックの終了です。このブロックはcheckGoal関数の結果がtrueだったとき、盤面がゴールしたときのブロックだったね。

37行目: if(checkSameBoard(new_state.board, check_list)がfalseと等しい)

　同じ盤面が過去にあったかをList型のcheck_listと照合します。最初の一回目はcheck_listは19行目で盤面の最初の形を保持してますねなので、次は新しい盤面を登録しないと行けないですね。

　ここで、38行目の穴埋めです。Queueクラスのexplore_queueとかListクラスのcheck_listとかのaddメソッドを使わないといけない感じだったね。38行目はexplore_queue.から始まってる穴埋めなのでexplore_queue.add(new_state)だな。

したがって、

キ　add(new_state)

が答えです。

　あとは39行目の穴埋めでcheck_list.で始めってる穴埋めなので、check_list(new_state.board)だな。start_state.boardで最初に探索する盤面は登録されてるし、stateだと盤面登録が遅れるので、stateで登録しちゃだめだよ。

したがって、

ク　add(new_state.board)

が答えです。

　実際に動かせるプログラムを作っても楽しいだろうね。ちょっと省略されてる部分が多いのでかなりの部分を補うプログラムになると思うけど。実際につくって公開したらバズバズバズバズでばずるんじゃないかな。情報処理技術者試験の問題をアプリにしましたでネットニュースいきだろう。スライドパズラーには重宝されるアプリになるに違いない。美しいUIが大事だろうね。WinとAndroidとiOS向けのものが作れたら十分だろうね。間違いなくバズるわ。保証するわ。あ、保証はできないか。でも、有料アプリとかにすると、炎上バズバズもありえるな。保証できないけど。


〇solveNPuzzle(整数型: board_size)
 BoardState: start_state /* 開始時点の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型配列の配列: goal_board /* ゴールの盤面配列 */
 整数型配列の配列: direction /* 駒の移動に伴う空白マスの移動方向を行番号の増減を1番目の要素、列番号の増減を2番目の要素で表現する配列 */
 Queue: explore_queue /* 探索対象の盤面を保持するキューのインスタンスへの参照 */
 List: check_list /* 探索済みの盤面配列を保持するリストのインスタンスへの参照 */
 BoardState: state /* 駒が移動する前の盤面を保持するBoardStateのインスタンスへの参照 */
 BoardState: new_state /* 駒が移動した後の盤面を保持するBoardStateのインスタンスへの参照 */
 整数型: change_num /* 移動する駒の数字 */
 整数型: i /* forループ内で使用するカウンタ変数 */
 start_state ← BoardState() 
 goal_board ← createGoal(board_size) 
 start_state.board ← createStart(board_size) 
 start_state.space ← getSpace(start_state.board) 
 direction ← {{1, 0}, {0, -1}, {-1, 0}, {0, 1}} 
 explore_queue ← Queue() 
 explore_queue.add(start_state) 
 check_list ← List() 
 check_list.add(start_state.board) 
 while(explore_queue.isEmpty()がfalseと等しい) 
   state ← explore_queue.poll()
   for(iを1からdirectionの要素数まで1ずつ増やす) 
     if((state.space[1] + direction[i][1] が1以上) かつ 
        (state.space[1] + direction[i][1] が board_size 以下) かつ 
        (state.space[2] + direction[i][2] が1以上) かつ 
        (state.space[2] + direction[i][2] が board_size 以下)) 
       new_state ← BoardState(state) 
       new_state.space[1] ← state.space[1] + direction[i][1]
       new_state.space[2] ← state.space[2] + direction[i][2]
       change_num ← new_state.board[new_state.space[1]][new_state.space[2]]
       new_state.board[new_state.space[1]][new_state.space[2]] ← board_size * board_size 
       new_state.boart[state.space[1]][state.space[2]] ← change_num 
       if(checkGoal(new_state.board, goal_board)がtrueと等しい) 
         printResult(new_state) 
         return 
       endif 
       if(checkSameBoard(new_state.board, check_list)がfalseと等しい) 
         explore_queue.add(new_state) 
         check_list.add(new_state.board) 
       endif 
     endif 
   endfor 
 endwhile 
 ゴールの盤面に至る駒の移動方法がない旨のメッセージを出力 
 return

　ちな、ルートノードが終わった後は③の盤面で空白マスの交換ができるのを探して、⑪以下の子ノードの探索をして、→②→⑨→⑨の子ノード→⑧→⑧の子ノード→⑦→⑦の子ノード→⑥→⑥の子ノード→①→④→④の子ノードという順番で処理が進んでいくのかなと思います。

AP過去問_令和7年度春期_午後_問2_経営戦略の同じ回の前の問題へ移動。

AP過去問_令和7年度春期_午後_問4_システムアーキテクチャの同じ回の次の問題へ移動。

AP過去問_令和6年度秋期_午後_問3_プログラミングの前の回の同じカテゴリの問題へ移動。

AP 過去問題午後に戻る。

令和7年度春期 午後 問3 プログラミング(AIプロンプト向け)

令和7年度春期 午後 問3 プログラミング(問題原文)

回答・解説

令和7年度春期午後問3 プログラミング(AIプロンプト向け)

令和7年度春期午後問3 プログラミング(問題原文)