「AP過去問 令和7年度春期 午前 問21」の版間の差分
(ページの作成:「AP過去問 令和7年度春期 午前 問題に戻る AP過去問 令和7年度春期 午前 問20前の問題へ AP過去問 令和7年度春期 午前 問22次の問題へ =='''問21(問題文)'''== ア イ ウ エ =='''回答・解説'''== AP過去問 令和7年度春期 午前 問20前の問題へ AP過去問 令和7年度春期 午前 問22次の問題…」) |
編集の要約なし |
||
| (同じ利用者による、間の7版が非表示) | |||
| 1行目: | 1行目: | ||
<freescript></script><script type="text/x-mathjax-config"> | |||
MathJax.Ajax.config.path["Contrib"]="https://wiki.yo-net.jp/mathjax/"; | |||
MathJax.Hub.Register.StartupHook("TeX Jax Ready",function (){ | |||
MathJax.Hub.Insert( | |||
MathJax.InputJax.TeX.Definitions.macros,{ | |||
cancel: ["Extension","cancel"], | |||
bcancel: ["Extension","cancel"], | |||
xcancel: ["Extension","cancel"], | |||
cancelto: ["Extension","cancel"] | |||
} | |||
); | |||
}); | |||
MathJax.Hub.Config({ | |||
tex2jax:{ | |||
displayMath: [['$$', '$$'],['\\[', '\\]']], //displayスタイル数式に利用する記号の指定 | |||
inlineMath: [['\\@', '\\@'],['\\(', '\\)']],//inlineスタイル数式に利用する記号の指定 | |||
//ここは使う人が自由に設定する部分です。 | |||
processEscapes: true | |||
}, | |||
TeX:{ | |||
// equationNumbers:{autoNumber: "AMS"}, | |||
extensions: ["[Contrib]/physics/physics.js","[Contrib]/siunitx/siunitx.js", "color.js", "cancel.js"] | |||
}, | |||
"HTML-CSS": { | |||
availableFonts: [], | |||
preferredFont: null, | |||
webFont: "Neo-Euler" | |||
}, | |||
}); | |||
</script> | |||
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.9/MathJax.js?config=TeX-AMS_HTML-full"></script> | |||
<script></freescript> | |||
<freescript></script> | |||
<style> | |||
.table-container { | |||
display: inline-block; | |||
text-align: left; | |||
margin: 20px; | |||
} | |||
.table-header { | |||
display: flex; | |||
justify-content: space-between; | |||
margin-bottom: 5px; | |||
} | |||
</style> | |||
<style> | |||
div.imadake-left mjx-container[jax="CHTML"][display="true"]{text-align: left;} | |||
.imadake-left .MathJax_Display { | |||
text-align: left !important; | |||
font-size: 0.9rem; | |||
} | |||
</style> | |||
<script></freescript> | |||
[[AP過去問 令和7年度春期 午前#問題|AP過去問 令和7年度春期 午前 問題]]に戻る | [[AP過去問 令和7年度春期 午前#問題|AP過去問 令和7年度春期 午前 問題]]に戻る | ||
| 8行目: | 62行目: | ||
=='''問21(問題文)'''== | =='''問21(問題文)'''== | ||
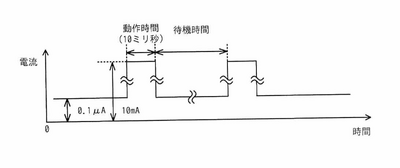
loT システムにおいて、センサーの値をゲートウェイに送信するセンサーノードの消費電流を抑えるため、図のような間欠動作を考える。センサーノードの動作時間は10ミリ秒で,その間は平均して10mAの電流が流れる。待機中は常に0. 1μAの電流が流れる。間欠動作の平均電流を1μA以下にするための待機時間として、最も短いものはどれか。ここで、平均電流の値を求める時間は十分に長いものとする。 | |||
[[ファイル:AP R7 1Spring AMQ21 Fig1.png|400px||none|]] | |||
ア 1.1秒 | |||
イ 11.1秒 | |||
ウ 111.1秒 | |||
エ 1111.1秒 | |||
=='''回答・解説'''== | =='''回答・解説'''== | ||
全体の平均電流を1μAにしたいので、 | |||
<freescript></script> | |||
<div class="imadake-left" align="left"> | |||
$$ | |||
\require{enclose} | |||
\begin{eqnarray} | |||
\frac{動作時の電流 \times 時間 + 待機時の電流 \times 時間\phantom{ }}{全体の時間} = 1 \text{[μA]} | |||
\end{eqnarray} | |||
$$ | |||
</div> | |||
<script></freescript> | |||
<freescript></script> | |||
<div class="imadake-left" align="left"> | |||
$$ | |||
\require{enclose} | |||
\begin{eqnarray} | |||
\frac{10,000 \times 10 + 0.1 \times T}{10 + T} = 1 | |||
\end{eqnarray} | |||
$$ | |||
</div> | |||
<script></freescript> | |||
この方程式を解くと: | |||
<freescript></script> | |||
<div class="imadake-left" align="left"> | |||
$$ | |||
\require{enclose} | |||
\begin{eqnarray} | |||
\frac{100,000 + 0.1T}{10 + T} = 1 | |||
\end{eqnarray} | |||
$$ | |||
</div> | |||
<script></freescript> | |||
両辺に(10+T)をかけて: | |||
<span style="font-size: 0.9rem;">\( 100,000 + 0.1T = 10 + T \)</span> | |||
<span style="font-size: 0.9rem;">\( 100,000−10=T−0.1T \)</span> | |||
<span style="font-size: 0.9rem;">\( 0.9T = 99,990 \)</span> | |||
<span style="font-size: 0.9rem;">\( T = \frac{99,9900}{9}=111,100 \)</span> | |||
<span style="font-size: 0.9rem;">\( T = 111,100 \text{[ミリ秒]}\)</span> | |||
<span style="font-size: 0.9rem;">\( T = 111.1 \text{[秒]}\)</span> | |||
したがって | |||
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; "> | |||
ウ</span> | |||
が答えです。 | |||
2025年4月25日 (金) 00:48時点における最新版
AP過去問 令和7年度春期 午前 問20前の問題へ
AP過去問 令和7年度春期 午前 問22次の問題へ
問21(問題文)
loT システムにおいて、センサーの値をゲートウェイに送信するセンサーノードの消費電流を抑えるため、図のような間欠動作を考える。センサーノードの動作時間は10ミリ秒で,その間は平均して10mAの電流が流れる。待機中は常に0. 1μAの電流が流れる。間欠動作の平均電流を1μA以下にするための待機時間として、最も短いものはどれか。ここで、平均電流の値を求める時間は十分に長いものとする。
ア 1.1秒
イ 11.1秒
ウ 111.1秒
エ 1111.1秒
回答・解説
全体の平均電流を1μAにしたいので、
$$ \require{enclose} \begin{eqnarray} \frac{動作時の電流 \times 時間 + 待機時の電流 \times 時間\phantom{ }}{全体の時間} = 1 \text{[μA]} \end{eqnarray} $$
$$ \require{enclose} \begin{eqnarray} \frac{10,000 \times 10 + 0.1 \times T}{10 + T} = 1 \end{eqnarray} $$
この方程式を解くと:
$$ \require{enclose} \begin{eqnarray} \frac{100,000 + 0.1T}{10 + T} = 1 \end{eqnarray} $$
両辺に(10+T)をかけて:
\( 100,000 + 0.1T = 10 + T \)
\( 100,000−10=T−0.1T \)
\( 0.9T = 99,990 \)
\( T = \frac{99,9900}{9}=111,100 \)
\( T = 111,100 \text{[ミリ秒]}\)
\( T = 111.1 \text{[秒]}\)
したがって
ウ
が答えです。
AP過去問 令和7年度春期 午前 問20前の問題へ
AP過去問 令和7年度春期 午前 問22次の問題へ