AP過去問 令和6年度秋期 午前 問14

|AP過去問 令和6年度秋期 午前 問題に戻る

AP過去問 令和6年度秋期 午前 問13へ

AP過去問 令和6年度秋期 午前 問15へ

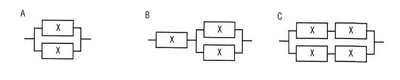
問14(問題文)

　稼働率が等しい装置Xを直列や並列に組み合わせたとき、システム全体の稼働率を高い順に並べたものはどれか。ここで、装置Xの稼働率は0よりも大きく1未満である。

ア　A, B, C

イ　A, C, B

ウ　C, A, B

エ　C, B, A

　

回答・解説

　稼働率は直列だとそれぞれの稼働率の積で算出されます。並列の場合は、1-(1-稼働率)×(1-稼働率)で算出されます。1-稼働率というのは故障率で、両方が故障する確率が故障率の積で算出され、算出した並列時の同時故障率を全体の確率1との差で導き出されます。例えば、Xの稼働率を0.8として考えてみましょう。

A

は並列になった稼働率なので以下の式で求められ計算をすすめると

$1-(1-0.8)\cdot (1-0.8)$

$=1-(0.2)\cdot (0.2)$

$=1-(0.04)$

$=9.96$

B

はAで求めたカタチにさらにXが直列になっているので以下の式で求められ計算をすすめると

$0.8\cdot 9.96$

$=7.968$

C

は直列のXが並列になっているので

$0.8\cdot 0.8$

$=0.64$

とまずは、直列のXの稼働率を求めてから

$1-(1-0.64)\cdot (1-0.64)$

$=1-(0.36)\cdot (0.36)$

$=1-0.1296$

$=0.8704$

　です。

　したがって、

イ　A, C, B

　が答えです。計算しなくても、並列は稼働率が高くなり、直列は稼働率が低くなるという法則だけでも今回のような問題なら答えを導き出すことができるようになります。そのあたりの思考力も高めると時間の節約になるでしょう。

　

AP過去問 令和6年度秋期 午前 問13へ

AP過去問 令和6年度秋期 午前 問15へ

|AP過去問 令和6年度秋期 午前 問題に戻る