「AP過去問 令和6年度秋期 午前 問14」の版間の差分
編集の要約なし |
編集の要約なし |
||
| 1行目: | 1行目: | ||
<yjavascript> | |||
<script type='text/x-mathjax-config'> | |||
MathJax = { | |||
tex: { | |||
packages: ['base'], // extensions to use | |||
inlineMath: [ // start/end delimiter pairs for in-line math | |||
['\\(', '\\)'] | |||
], | |||
displayMath: [ // start/end delimiter pairs for display math | |||
['$$', '$$'], | |||
['\\[', '\\]'] | |||
], | |||
processEscapes: true, // use \$ to produce a literal dollar sign | |||
processEnvironments: true, // process \begin{xxx}...\end{xxx} outside math mode | |||
processRefs: true, // process \ref{...} outside of math mode | |||
digits: /^(?:[0-9]+(?:\{,\}[0-9]{3})*(?:\.[0-9]*)?|\.[0-9]+)/, | |||
// pattern for recognizing numbers | |||
tags: 'none', // or 'ams' or 'all' | |||
tagSide: 'right', // side for \tag macros | |||
tagIndent: '0.8em', // amount to indent tags | |||
useLabelIds: true, // use label name rather than tag for ids | |||
multlineWidth: '85%', // width of multline environment | |||
maxMacros: 1000, // maximum number of macro substitutions per expression | |||
maxBuffer: 5 * 1024, // maximum size for the internal TeX string (5K) | |||
baseURL: // URL for use with links to tags (when there is a <base> tag in effect) | |||
(document.getElementsByTagName('base').length === 0) ? | |||
'' : String(document.location).replace(/#.*$/, '')) | |||
} | |||
"HTML-CSS": { | |||
availableFonts :[], | |||
preferredFont: null, | |||
webFont :"Neo-Euler" | |||
} | |||
}; | |||
</script> | |||
<script src="https://polyfill.io/v3/polyfill.min.js?features=es6"></script> | |||
<script id="MathJax-script" async src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script> | |||
</yjavascript> | |||
[[AP過去問 令和6年度秋期 午前#問題||AP過去問 令和6年度秋期 午前 問題]]に戻る | [[AP過去問 令和6年度秋期 午前#問題||AP過去問 令和6年度秋期 午前 問題]]に戻る | ||
2024年11月27日 (水) 00:22時点における版
問14(問題文)
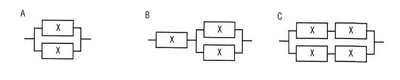
稼働率が等しい装置Xを直列や並列に組み合わせたとき、システム全体の稼働率を高い順に並べたものはどれか。ここで、装置Xの稼働率は0よりも大きく1未満である。
ア A, B, C
イ A, C, B
ウ C, A, B
エ C, B, A
回答・解説
稼働率は直列だとそれぞれの稼働率の積で算出されます。並列の場合は、1-(1-稼働率)×(1-稼働率)で算出されます。1-稼働率というのは故障率で、両方が故障する確率が故障率の積で算出され、算出した並列時の同時故障率を全体の確率1との差で導き出されます。例えば、Xの稼働率を0.8として考えてみましょう。
A
は並列になった稼働率なので以下の式で求められ計算をすすめると
\( 1-(1-0.8) \dot (1-0.8) \)
\( =1-(0.2) \dot (0.2) \)
\( =1-(0.04) \)
\( =9.96 \)
B
はAで求めたカタチにさらにXが直列になっているので以下の式で求められ計算をすすめると
\( 0.8 \dot 9.96 \)
\( = 7.968 \)
C
は直列のXが並列になっているので
\( 0.8 \dot 0.8 \)
\( = 0.64 \)
とまずは、直列のXの稼働率を求めてから
\( 1 - (1 - 0.64) \dot (1 - 0.64) \)
\( = 1 - (0.36) \dot (0.36) \)
\( = 1 - 0.1296 \)
\( = 0.8704 \)
です。
したがって、
イ A, C, B
が答えです。