AP過去問 令和7年度春期 午前 問21

AP過去問 令和7年度春期 午前 問題に戻る

AP過去問 令和7年度春期 午前 問20前の問題へ

AP過去問 令和7年度春期 午前 問22次の問題へ

　

問21(問題文)

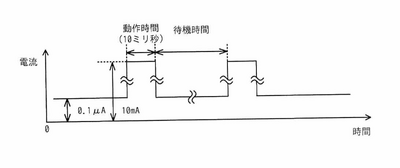
　loT システムにおいて、センサーの値をゲートウェイに送信するセンサーノードの消費電流を抑えるため、図のような間欠動作を考える。センサーノードの動作時間は10ミリ秒で，その間は平均して10mAの電流が流れる。待機中は常に0. 1μAの電流が流れる。間欠動作の平均電流を1μA以下にするための待機時間として、最も短いものはどれか。ここで、平均電流の値を求める時間は十分に長いものとする。

ア　1.1秒

イ　11.1秒

ウ　111.1秒

エ　1111.1秒

　

回答・解説

全体の平均電流を1μAにしたいので、

$$\require{enclose} \begin{eqnarray} \frac{動作時の電流 \times 時間 + 待機時の電流 \times 時間\phantom{　　}}{全体の時間} = 1 \text{[μA]} \end{eqnarray}$$

$$\require{enclose} \begin{eqnarray} \frac{10,000 \times 10 + 0.1 \times T}{10 + T} = 1 \end{eqnarray}$$

この方程式を解くと：

$$\require{enclose} \begin{eqnarray} \frac{100,000 + 0.1T}{10 + T} = 1 \end{eqnarray}$$

両辺に(10+T)をかけて：

$100,000 + 0.1T = 10 + T$

$100,000−10=T−0.1T$

$0.9T = 99,990$

$T = \frac{99,9900}{9}=111,100$

$T = 111,100 \text{[ミリ秒]}$

$T = 111.1 \text{[秒]}$

　

AP過去問 令和7年度春期 午前 問20前の問題へ

AP過去問 令和7年度春期 午前 問22次の問題へ

AP過去問 令和7年度春期 午前 問題に戻る