「AP過去問 令和7年度春期 午前 問6」の版間の差分
(ページの作成:「AP過去問 令和7年度春期 午前 問題に戻る AP過去問 令和7年度春期 午前 問5前の問題へ AP過去問 令和7年度春期 午前 問7次の問題へ =='''問6(問題文)'''== ア イ ウ エ =='''回答・解説'''== AP過去問 令和7年度春期 午前 問5前の問題へ AP過去問 令和7年度春期 午前 問7次の問題へ […」) |
(→回答・解説) |
||
| (同じ利用者による、間の9版が非表示) | |||
| 8行目: | 8行目: | ||
=='''問6(問題文)'''== | =='''問6(問題文)'''== | ||
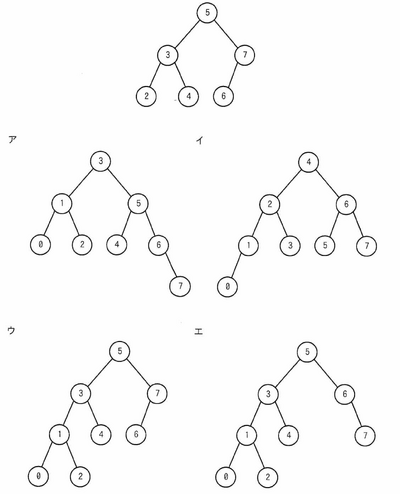
図の2分探索木に1と0の二つの要素を順に追加したAVL木として、適切なものはどれか。 | |||
[[ファイル:AP R7 1Spring AMQ6 Fig1.png|400px||none|]] | |||
=='''回答・解説'''== | |||
与えられた図の上部にある2分探索木(根が5の木)に対して、1と0をこの順序で挿入し、その後のAVL木(自己平衡二分探索木)として適切なものを選ぶ問題です。 | |||
AVL木は、'''Adelson-Velsky and Landis木'''の略です。 | |||
この名称は、1962年にこのデータ構造を提案したソビエト連邦の数学者、'''G.M. Adelson-Velsky''' 氏と '''E.M. Landis''' 氏の名前に由来しています。彼らが発表した論文「An algorithm for the organization of information」で紹介されました。 | |||
AVL木は、'''自己平衡二分探索木'''の最初の一つであり、各ノードにバランス係数(左右の部分木の高さの差)を保持し、その値が -1、0、+1 の範囲に収まるように挿入・削除時に回転操作を行うことで、常に木の高さを制御し、探索の効率を保つことを目的としています。 | |||
ノードの左と右の高さを調べて、すべてのノードにおいて-1、0、1となる場合は、バランスが崩れていないと判断できます。 | |||
1を追加すると、ノード2の左側にノード1として、追加することになります。なんで?2の左側にっていうのは木構造がそういうルールだからです。すべてのノードの左にはそのノードより小さい数だけが右には大きい数だけがぶら下がる決まりです。 | |||
では追加した後のそれぞれの左と右の高さを比べて、その差を見てみましょう。 | |||
ノード1は高さ0 | |||
ノード2の左は高さ1、右は無いから0で、1-0は1 | |||
ノード3の左は高さ2、右は1で2-1は1 | |||
ノード5の左は高さ3、右は2で3-2は1 | |||
ノード6は高さ0 | |||
ノード7は左は高さ1右はは0で1-0で1 | |||
すべて -1, 0, 1になってますので、この時点ではバランスが取れているので、1を追加する操作の後になにもやることはないです。 | |||
では、つづいて0を追加してみましょう。これはノード1の左に追加することになります。それでまた、高さの差について確認します。 | |||
ノード0は高さ0 | |||
ノード1の左は高さ1、右は無いから0で、1-0は1 | |||
ノード2の左は高さ2、右は無いから0で、2-0は2 | |||
ノード3の左は高さ3、右は1で3-1は2 | |||
ノード5の左は高さ4、右は2で4-2は2 | |||
ノード6は高さ0 | |||
ノード7は左は高さ1右はは0で1-0で1 | |||
すべて -1, 0, 1にはなっていません。バランスが崩れたので、操作が必要です。 | |||
'''左-左型(LL型)'''の不均衡なので、'''「右回転(Right Rotation)」'''でバランスを取ります。 | |||
ノード1をノード2の位置に移動して、ノード2はノード1の右に子として接続します。ノード0はノード1の左側の子の状態になります。 | |||
したがって答えは、 | |||
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; "> | |||
ウ</span> | |||
が答えです。 | |||
<yjavascript></script> | |||
<style> | |||
.db_table-wrapper { | |||
width: 100%; | |||
margin: auto; | |||
} | |||
.db_table { | |||
width: 100%; | |||
border-collapse: collapse; | |||
box-shadow: 0 4px 8px rgba(0,0,0,0.1); | |||
background-color: #fff; | |||
border-radius: 12px; | |||
overflow: hidden; | |||
} | |||
.db_table th, | |||
.db_table td { | |||
padding: 1rem; | |||
text-align: left; | |||
} | |||
.db_table th { | |||
background-color: #f0f0f0; | |||
font-weight: bold; | |||
} | |||
.db_table tr:not(:last-child) { | |||
border-bottom: 1px solid #e0e0e0; | |||
} | |||
.db_table tr:hover { | |||
background-color: #f5f5f5; | |||
} | |||
.db_caption { | |||
caption-side: top; | |||
padding: 1rem; | |||
font-size: 1.25rem; | |||
font-weight: bold; | |||
} | |||
</style> | |||
<div class="db_table-wrapper"> | |||
<table class="db_table"> | |||
<caption class="db_caption">AVL木の4種類の回転操作</caption> | |||
<thead> | |||
<tr> | |||
<th>不均衡の種類</th> | |||
<th>不均衡の原因</th> | |||
<th>必要な操作</th> | |||
<th>説明</th> | |||
</tr> | |||
</thead> | |||
<tbody> | |||
<tr> | |||
<td>'''LL型'''(左-左)</td> | |||
<td>左部分木の左に追加</td> | |||
<td>'''右回転'''(Right Rotation)</td> | |||
<td>単純な右回転で修正</td> | |||
</tr> | |||
<tr> | |||
<td>'''RR型'''(右-右)</td> | |||
<td>右部分木の右に追加</td> | |||
<td>'''左回転'''(Left Rotation)</td> | |||
<td>単純な左回転で修正</td> | |||
</tr> | |||
<tr> | |||
<td>'''LR型'''(左-右)</td> | |||
<td>左部分木の右に追加</td> | |||
<td>'''左回転 → 右回転'''</td> | |||
<td>左部分木を左回転してから、親を右回転</td> | |||
</tr> | |||
<tr> | |||
<td>'''RL型'''(右-左)</td> | |||
<td>右部分木の左に追加</td> | |||
<td>'''右回転 → 左回転'''</td> | |||
<td>右部分木を右回転してから、親を左回転</td> | |||
</tr> | |||
</tbody> | |||
</table> | |||
</div> | |||
<script></yjavascript> | |||
LL型 | |||
Z | |||
/ | |||
Y | |||
/ | |||
X | |||
Y | |||
/ \ | |||
X Z | |||
RR型 | |||
Z | |||
\ | |||
Y | |||
\ | |||
X | |||
Y | |||
/ \ | |||
Z X | |||
LR型 | |||
Z | |||
/ | |||
Y | |||
\ | |||
X | |||
X | |||
/ \ | |||
Y Z | |||
RL型 | |||
Z | |||
\ | |||
Y | |||
/ | |||
X | |||
X | |||
/ \ | |||
Z Y | |||
2025年4月23日 (水) 23:06時点における最新版
AP過去問 令和7年度春期 午前 問5前の問題へ
AP過去問 令和7年度春期 午前 問7次の問題へ
問6(問題文)
図の2分探索木に1と0の二つの要素を順に追加したAVL木として、適切なものはどれか。
回答・解説
与えられた図の上部にある2分探索木(根が5の木)に対して、1と0をこの順序で挿入し、その後のAVL木(自己平衡二分探索木)として適切なものを選ぶ問題です。
AVL木は、Adelson-Velsky and Landis木の略です。
この名称は、1962年にこのデータ構造を提案したソビエト連邦の数学者、G.M. Adelson-Velsky 氏と E.M. Landis 氏の名前に由来しています。彼らが発表した論文「An algorithm for the organization of information」で紹介されました。
AVL木は、自己平衡二分探索木の最初の一つであり、各ノードにバランス係数(左右の部分木の高さの差)を保持し、その値が -1、0、+1 の範囲に収まるように挿入・削除時に回転操作を行うことで、常に木の高さを制御し、探索の効率を保つことを目的としています。
ノードの左と右の高さを調べて、すべてのノードにおいて-1、0、1となる場合は、バランスが崩れていないと判断できます。
1を追加すると、ノード2の左側にノード1として、追加することになります。なんで?2の左側にっていうのは木構造がそういうルールだからです。すべてのノードの左にはそのノードより小さい数だけが右には大きい数だけがぶら下がる決まりです。
では追加した後のそれぞれの左と右の高さを比べて、その差を見てみましょう。
ノード1は高さ0
ノード2の左は高さ1、右は無いから0で、1-0は1
ノード3の左は高さ2、右は1で2-1は1
ノード5の左は高さ3、右は2で3-2は1
ノード6は高さ0
ノード7は左は高さ1右はは0で1-0で1
すべて -1, 0, 1になってますので、この時点ではバランスが取れているので、1を追加する操作の後になにもやることはないです。
では、つづいて0を追加してみましょう。これはノード1の左に追加することになります。それでまた、高さの差について確認します。
ノード0は高さ0
ノード1の左は高さ1、右は無いから0で、1-0は1
ノード2の左は高さ2、右は無いから0で、2-0は2
ノード3の左は高さ3、右は1で3-1は2
ノード5の左は高さ4、右は2で4-2は2
ノード6は高さ0
ノード7は左は高さ1右はは0で1-0で1
すべて -1, 0, 1にはなっていません。バランスが崩れたので、操作が必要です。
左-左型(LL型)の不均衡なので、「右回転(Right Rotation)」でバランスを取ります。
ノード1をノード2の位置に移動して、ノード2はノード1の右に子として接続します。ノード0はノード1の左側の子の状態になります。
したがって答えは、
ウ
が答えです。
| 不均衡の種類 | 不均衡の原因 | 必要な操作 | 説明 |
|---|---|---|---|
| '''LL型'''(左-左) | 左部分木の左に追加 | '''右回転'''(Right Rotation) | 単純な右回転で修正 |
| '''RR型'''(右-右) | 右部分木の右に追加 | '''左回転'''(Left Rotation) | 単純な左回転で修正 |
| '''LR型'''(左-右) | 左部分木の右に追加 | '''左回転 → 右回転''' | 左部分木を左回転してから、親を右回転 |
| '''RL型'''(右-左) | 右部分木の左に追加 | '''右回転 → 左回転''' | 右部分木を右回転してから、親を左回転 |
LL型
Z
/
Y
/
X
Y / \ X Z
RR型
Z
\
Y
\
X
Y / \ Z X
LR型
Z
/
Y
\
X
X / \ Y Z
RL型
Z \ Y / X
X / \ Z Y
AP過去問 令和7年度春期 午前 問5前の問題へ
AP過去問 令和7年度春期 午前 問7次の問題へ