「AP過去問 令和6年度春期 午前 問5」の版間の差分
編集の要約なし |
(→回答・解説) |
||
| (同じ利用者による、間の4版が非表示) | |||
| 8行目: | 8行目: | ||
=='''問5(問題文)'''== | =='''問5(問題文)'''== | ||
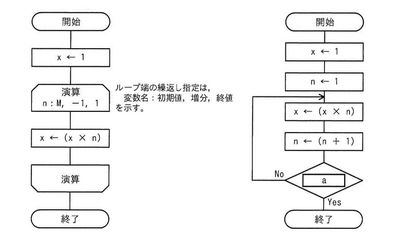
正の整数Mに対して、次の二つの流れ図に示すアルゴリズムを実行したとき、結果xの値が等しくなるようにしたい。aに入れる条件として、適切なものはどれか。 | |||
[[ファイル:AP R6 1Spring AMQ5 Fig1.png|400px|thumb|none|]] | |||
| 22行目: | 25行目: | ||
=='''回答・解説'''== | =='''回答・解説'''== | ||
まずは左のフローチャートの処理を眺めてみます。 | |||
例えばM=3の処理の場合を考えてみましょう。 | |||
xに1を格納した後 | |||
初期値がMで増分が-1で終わり値が1の変数nを使うループの宣言があって次の処理が | |||
x = n * xですから最初の演算は | |||
3 = 3 * 1 次は | |||
6 = 2 * 3 次は | |||
6 = 1 * 6 で処理終了です。 | |||
階乗の計算をしていますね。M=3のときは3! = 6を求めています。 | |||
では右のフローチャートをみてみましょう。 | |||
xに1、nに1を格納した後ループに突入します。 | |||
x = x * n ですから | |||
1 = 1 * 1 次に、n = n + 1、ですから | |||
2 = 1 + 1、この繰り返しで | |||
2 = 1 * 2 3 = 2 + 1、次に | |||
6 = 2 * 3 4 = 3 + 1、ここで処理を止めなければなりません。 | |||
このときnは4になっていて、Mは3ですから、このときはじめて成立する条件は | |||
n > M です。 4 > 3 が成立するので、YESの方の分岐に進むことができます。 | |||
したがって、 | |||
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; "> | |||
ウ n > M</span> | |||
が答えです。 | |||
2025年1月27日 (月) 02:00時点における最新版
AP過去問 令和6年度春期 午前 問4前の問題へ
AP過去問 令和6年度春期 午前 問6次の問題へ
問5(問題文)
正の整数Mに対して、次の二つの流れ図に示すアルゴリズムを実行したとき、結果xの値が等しくなるようにしたい。aに入れる条件として、適切なものはどれか。
ア n < M
イ n > M-1
ウ n > M
エ n > M+1
回答・解説
まずは左のフローチャートの処理を眺めてみます。
例えばM=3の処理の場合を考えてみましょう。
xに1を格納した後
初期値がMで増分が-1で終わり値が1の変数nを使うループの宣言があって次の処理が
x = n * xですから最初の演算は
3 = 3 * 1 次は
6 = 2 * 3 次は
6 = 1 * 6 で処理終了です。
階乗の計算をしていますね。M=3のときは3! = 6を求めています。
では右のフローチャートをみてみましょう。
xに1、nに1を格納した後ループに突入します。
x = x * n ですから
1 = 1 * 1 次に、n = n + 1、ですから
2 = 1 + 1、この繰り返しで
2 = 1 * 2 3 = 2 + 1、次に
6 = 2 * 3 4 = 3 + 1、ここで処理を止めなければなりません。
このときnは4になっていて、Mは3ですから、このときはじめて成立する条件は
n > M です。 4 > 3 が成立するので、YESの方の分岐に進むことができます。
したがって、
ウ n > M
が答えです。
AP過去問 令和6年度春期 午前 問4前の問題へ
AP過去問 令和6年度春期 午前 問6次の問題へ