「Python matplotlibを使って学ぶ統計処理 正規分布」の版間の差分
| (同じ利用者による、間の12版が非表示) | |||
| 1行目: | 1行目: | ||
<yjavascript> | <yjavascript> | ||
<!--<script type='text/x-mathjax-config'> | |||
MathJax.Hub.Config({ | |||
"tex2jax" :{ | |||
packages: ['base'], // extensions to use | |||
inlineMath: [ // start/end delimiter pairs for in-line math | |||
['\\(', '\\)'] | |||
], | |||
displayMath: [ // start/end delimiter pairs for display math | |||
['$$', '$$'], | |||
['\\[', '\\]'] | |||
], | |||
}, | |||
"TeX" : { | |||
extentions :["color.js", "cancel.js"], | |||
}, | |||
"HTML-CSS": { | |||
availableFonts :[], | |||
webFont :"Neo-Euler", | |||
} | |||
}); | |||
</script> | |||
<script type='text/javascript' src='https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML%2CSafe.js&ver=3.8'> | |||
</script>--> | |||
<script type='text/x-mathjax-config'> | <script type='text/x-mathjax-config'> | ||
MathJax = { | MathJax = { | ||
| 27行目: | 50行目: | ||
'' : String(document.location).replace(/#.*$/, '')) | '' : String(document.location).replace(/#.*$/, '')) | ||
} | } | ||
"HTML-CSS": { | |||
availableFonts :[], | |||
preferredFont: null, | |||
webFont :"Neo-Euler" | |||
} | |||
}; | }; | ||
</script> | </script> | ||
| 48行目: | 76行目: | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "background-color: #f2f6ff; white-space:nowrap; padding:5px; border: dotted 1px black; border-radius: 10px;" | <big>$$ f( x) \ =\ \frac{1}{\sqrt{2\pi } \sigma }\exp^{-\frac{1}{2\sigma } (x-\mu )^{2}} $$ | | style= "background-color: #f2f6ff; white-space:nowrap; padding:5px; border: dotted 1px black; border-radius: 10px;" | <big>$$ f( x) \ =\ \frac{1}{\sqrt{2\pi } \sigma }\exp^{-\frac{1}{2\sigma } (x-\mu )^{2}} $$ </big> | ||
|} | |} | ||
| 87行目: | 115行目: | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> | | style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> $$ \int e^{-x^2} \cdot dx = \sqrt{\pi}$$ </big> | ||
|} | |} | ||
| 95行目: | 123行目: | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> | | style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> $$ \int e^{-\mathrm{N}x^2} \cdot dx = \sqrt{\frac{\mathstrut\pi}{\mathstrut \mathrm{N}}} \tag{1} $$ </big> | ||
|} | |} | ||
| 107行目: | 135行目: | ||
さてさて、証明を理解したとして、\( (1) \)の式の両辺に\( \sqrt{\frac{\mathrm{N}}{\pi}} \)を掛けて | さてさて、証明を理解したとして、\( (1) \)の式の両辺に\( \sqrt{\frac{\mathrm{N}}{\pi}} \)を掛けて | ||
<big> | <big> $$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut\pi}} e^{-\mathrm{N}x^2} \cdot dx = \sqrt{\frac{\mathstrut\pi}{\mathstrut \mathrm{N}}}\sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}}= 1 $$ </big> | ||
| 113行目: | 141行目: | ||
<big> | <big> $$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}} e^{-\mathrm{N}(x-\mu)^2} \cdot dx = 1 $$ </big> | ||
==== 求めるべき係数の算出の前に〜確率密度関数から考える期待値・平均値と分散値について ==== | ==== 求めるべき係数の算出の前に〜確率密度関数から考える期待値・平均値と分散値について ==== | ||
<!--$ \tcdegree\tccelsius\tcperthousand\tcmu\tcohm $--> | |||
ここで、確率密度の関数の積分と確率密度関数と平均値<span>(</span>期待値<span>)</span>、分散の関係を纏めておきます。平均値と期待値はよく似ている表現ですが、期待値にはゆくゆくはそうなるだろうという収束する着地点を表し、平均値は過去の実際のデータが示す値をひらたくした値という意味合いが強いです。ここでは厳密な使い分けをせず使っています。え?こういう時って平均値じゃなくて期待値って単語をつかうんじゃね?とか、そういうのは本来の意味を理解した上で個々人で変換して下さい。こちらとして、どっちかの意味であるかを厳密にする必要がある場合は単語を使う前にことわりを入れます。え?それって間違った表現もしますって宣言しているんじゃね?とか思ったでしょう。そういうことです。でも時々、意味は違うんで意識します。くらいの感じです。え?それってやばくね。このページの正確さやばくね?まぁね。やばいね。でもね。気楽に考えようって事もあるんですよ。だってどういう題材を扱っているかは人の気持ち次第だし。全部のデータがそろっていて、そのことについて言っているのか、まだそろっていないこれからのことを含めて考えているのかなんてのは、その時の考え方次第だし、人それぞれ自由だと思うんです。 | ここで、確率密度の関数の積分と確率密度関数と平均値<span>(</span>期待値<span>)</span>、分散の関係を纏めておきます。平均値と期待値はよく似ている表現ですが、期待値にはゆくゆくはそうなるだろうという収束する着地点を表し、平均値は過去の実際のデータが示す値をひらたくした値という意味合いが強いです。ここでは厳密な使い分けをせず使っています。え?こういう時って平均値じゃなくて期待値って単語をつかうんじゃね?とか、そういうのは本来の意味を理解した上で個々人で変換して下さい。こちらとして、どっちかの意味であるかを厳密にする必要がある場合は単語を使う前にことわりを入れます。え?それって間違った表現もしますって宣言しているんじゃね?とか思ったでしょう。そういうことです。でも時々、意味は違うんで意識します。くらいの感じです。え?それってやばくね。このページの正確さやばくね?まぁね。やばいね。でもね。気楽に考えようって事もあるんですよ。だってどういう題材を扱っているかは人の気持ち次第だし。全部のデータがそろっていて、そのことについて言っているのか、まだそろっていないこれからのことを含めて考えているのかなんてのは、その時の考え方次第だし、人それぞれ自由だと思うんです。 | ||
| 122行目: | 150行目: | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big | | style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big><span>累積確率密度 </span> $$ 1 = \int f(x) \cdot dx $$ <span>平均値</span> $$\mu = \int x \cdot f(x) \cdot dx $$ <span>分散</span> $$\sigma^{2} = \int (x-\mu)^{2} \cdot f(x) \cdot dx $$ </big> | ||
|} | |} | ||
| 133行目: | 161行目: | ||
確率密度関数で積分して1となる面積にデータである\( x \)を掛ければ面積が平均値と一致します。確率密度の関数のパラメータの\( \sigma \)を\( 1 \)に固定すれば、上記のグラフのように\( \mu \)がプラスの時は上側にコブが出来るグラフでマイナスのときは下側にコブが出来るグラフになります。もちろん面積は\( \mu \)と同じ値になります。\( \mu \)が大きいほど大きいコブになって面積が大きくなっていきます。マイナス側も同じで小さくなるほど、コブが下向きで大きくなってマイナスの面積が大きくなります。\( \mu \)が\( 0 \)のときだけ、\( f(x)=-x \)のグラフで対称となる小さなコブができた状態でプラス側では上向きにマイナス側では下向きにコブができます。面積合計は打ち消しあって0になります。なんで、正規分布の積分をする前の\( f(x) \)に対して\( x \)をかけてから積分すると、これほど都合よく平均値と一致させることができるのか?確かめる必要があります。では少し確認してみることにしましょう。 | 確率密度関数で積分して1となる面積にデータである\( x \)を掛ければ面積が平均値と一致します。確率密度の関数のパラメータの\( \sigma \)を\( 1 \)に固定すれば、上記のグラフのように\( \mu \)がプラスの時は上側にコブが出来るグラフでマイナスのときは下側にコブが出来るグラフになります。もちろん面積は\( \mu \)と同じ値になります。\( \mu \)が大きいほど大きいコブになって面積が大きくなっていきます。マイナス側も同じで小さくなるほど、コブが下向きで大きくなってマイナスの面積が大きくなります。\( \mu \)が\( 0 \)のときだけ、\( f(x)=-x \)のグラフで対称となる小さなコブができた状態でプラス側では上向きにマイナス側では下向きにコブができます。面積合計は打ち消しあって0になります。なんで、正規分布の積分をする前の\( f(x) \)に対して\( x \)をかけてから積分すると、これほど都合よく平均値と一致させることができるのか?確かめる必要があります。では少し確認してみることにしましょう。 | ||
<big> | <big>$$ \int^{\infty}_{-\infty} f(x)\cdot dx = \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$</big> | ||
のような形式が正規分布の関数で、一番最初に示した求めるべき結果でした。まだ証明していないのに利用するのはずるいですが、これに\( x \)をかけると | のような形式が正規分布の関数で、一番最初に示した求めるべき結果でした。まだ証明していないのに利用するのはずるいですが、これに\( x \)をかけると | ||
<big> | <big>$$ \int^{\infty}_{-\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$</big> | ||
上記の式が平均値を求める式で、それってあってるの?という探究の始まりした。ここで、\( z = \frac{x -\mu}{\sigma} \)…<span>(</span>2<span>)</span>という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… <span>(</span>3<span>)</span>で、 <span>(</span>2<span>)</span>および<span>(</span>3<span>)</span>の式を当てはめると | 上記の式が平均値を求める式で、それってあってるの?という探究の始まりした。ここで、\( z = \frac{x -\mu}{\sigma} \)…<span>(</span>2<span>)</span>という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… <span>(</span>3<span>)</span>で、 <span>(</span>2<span>)</span>および<span>(</span>3<span>)</span>の式を当てはめると | ||
<big> | <big>$$ \int^{\infty}_{-\infty}\textcolor{red}{x(←(3)式)} \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\textcolor{blue}{\sigma^{2}}}\textcolor{blue}{(x-\mu)^{2}(←(2)式)}}\cdot dx $$</big> | ||
を上記のように適用すると | を上記のように適用すると | ||
<big> | <big>$$ \int^{\infty}_{-\infty} (\textcolor{red}{z \cdot \sigma + \mu}) \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$</big> | ||
となります。\( \sigma \)に斜線が入っているのは後で置換積分の間違いに気付いたもので、あえて記録を残しています。後ほど細かい説明をしています。 <span>(</span>2<span>)</span>式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して | となります。\( \sigma \)に斜線が入っているのは後で置換積分の間違いに気付いたもので、あえて記録を残しています。後ほど細かい説明をしています。 <span>(</span>2<span>)</span>式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して | ||
<big> | <big>$$ \textcolor{green}{\int^{\infty}_{-\infty} z \cdot \sigma \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz} + \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
上記のようになり、<span style="color: green;">2つの積分の和の構造の最初の積分の部分<span>(</span>緑<span>)</span></span>はちょっと確かめれば原点を通過する奇関数と呼ばれる形式になっています。要するに積分をすると0になるということです。グラフをプロットして確かめてみると以下の通りです。 | 上記のようになり、<span style="color: green;">2つの積分の和の構造の最初の積分の部分<span>(</span>緑<span>)</span></span>はちょっと確かめれば原点を通過する奇関数と呼ばれる形式になっています。要するに積分をすると0になるということです。グラフをプロットして確かめてみると以下の通りです。 | ||
[[ファイル: ZsigmaNormalDistdz ZeroEvi Fit.png |650px|||ゼロになることを示すグラフ]] | [[ファイル: ZsigmaNormalDistdz ZeroEvi Fit.png |650px|||ゼロになることを示すグラフ]] | ||
<big> | <big>$$ 0 + \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
と、上記のように定数\( \mu \)倍を使って積分する式になります。そうすると上記の式から\( \mu \)を除いた部分 | と、上記のように定数\( \mu \)倍を使って積分する式になります。そうすると上記の式から\( \mu \)を除いた部分 | ||
<big> | <big>$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
は確率密度関数で積分<span>(</span>グラフのプロットとy=0に囲まれた部分面積を求める操作でマイナス領域とプラス領域の差し引きをする<span>)</span>をすると1になるものですから、最終的には | は確率密度関数で積分<span>(</span>グラフのプロットとy=0に囲まれた部分面積を求める操作でマイナス領域とプラス領域の差し引きをする<span>)</span>をすると1になるものですから、最終的には | ||
<big> | <big>$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz = 1 $$</big> | ||
で、先程示された式は定数\( \mu \)倍を使って積分する式\( \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz \)と表現することができます。確率密度関数の中の\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。 | で、先程示された式は定数\( \mu \)倍を使って積分する式\( \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz \)と表現することができます。確率密度関数の中の\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。 | ||
<big>\($ \mu \cdot 1 $\)</big> | <big>\($ \mu \cdot 1 $\)</big> | ||
となりますから、元々の式の計算結果は平均値を意味する\( \mu \)であると言えます。確率密度関数\( f(x) \)を\( x \)倍したものの積分は\( \mu \)になることが確認でき、 | となりますから、元々の式の計算結果は平均値を意味する\( \mu \)であると言えます。確率密度関数\( f(x) \)を\( x \)倍したものの積分は\( \mu \)になることが確認でき、 | ||
<big> | <big>$$ \mu = \int^{\infty}_{-\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$</big> | ||
<big> | <big>$$\mu = \int x \cdot f(x) \cdot dx $$</big> | ||
であると言えます。 | であると言えます。 | ||
| 166行目: | 194行目: | ||
とイメージだけでは怪しいので、確率密度関数に\( (x - \mu)^2 \)をかけたモノを積分するだけで分散が求まるのか、ここでも確認をしてみたいと思います。分散はデータを2乗したものの平均から平均値を2乗したものを引く | とイメージだけでは怪しいので、確率密度関数に\( (x - \mu)^2 \)をかけたモノを積分するだけで分散が求まるのか、ここでも確認をしてみたいと思います。分散はデータを2乗したものの平均から平均値を2乗したものを引く \( \sigma^2=\overline{\text{x}^{2}} -\overline{\text{x}}^{2} \) で求めることができます。本当にそれでも分散が算出できるのかについても触れないといけないですね。ここで\( \overline{\text{x}} \)は全部のデータ\( \text{x} \)に対するの平均を意味します。オーバーラインの下にあるモノに対しての平均になります。\( x \)は一つのデータで、与えられた\( x \)は分布関数\( f(x) \)の値によって表現される全体のデータ出現頻度に相当する数値となり、\( x \)のときの\( f(x) \)で囲われる面積によって確率が決定されるものなのでした。このことを踏まえて、説明を続けます。 | ||
\( \sigma^2=\overline{\text{x}^{2}} -\overline{\text{x}}^{2} \)が成り立つことについての確認として、4つのデータ\( x =\)個別のデータ変数\({a,b,c,d} \)においては | |||
<big> | <big>$$ xの平均値 \overline{x} = \frac{ \mathrm{a}+b+c+d}{4} $$</big> | ||
個別のデータを2乗したものを平均化する | 個別のデータを2乗したものを平均化する | ||
<big> | <big>$$ | ||
\begin{align} | \begin{align} | ||
x^2の平均値 \overline{x^2} = \frac{\unicode{x0061}^2+b ^2 +c ^2 +d ^2}{4} \nonumber | x^2の平均値 \overline{x^2} = \frac{\unicode{x0061}^2+b ^2 +c ^2 +d ^2}{4} \nonumber | ||
\end{align} | \end{align} | ||
$ | $$ </big> | ||
分散は個別のデータと平均値を引いたモノについて2乗して、それぞれ和にしたものをデータ数で割ったモノと定義されていますから、 | 分散は個別のデータと平均値を引いたモノについて2乗して、それぞれ和にしたものをデータ数で割ったモノと定義されていますから、 | ||
<big> | <big>$$ xの分散 \sigma^2 = \frac{(a-\overline{x})^2+ (b-\overline{x})^2 + (c-\overline{x})^2 + (d-\overline{x})^2}{4} $$ </big> | ||
となって、上記の2乗になっている部分を展開すると分配法則の\( (a + b)^2 = a^2 + 2ab + b^2 \)を利用して | となって、上記の2乗になっている部分を展開すると分配法則の\( (a + b)^2 = a^2 + 2ab + b^2 \)を利用して | ||
<big> | <big>$$ = \frac{( a^2-2a\overline{x}+\overline{x}^2) + (b^2-2b\overline{x}+\overline{x}^2) + (c^2-2c\overline{x}+\overline{x}^2) + (d^2-2d\overline{x}+\overline{x}^2)}{4} $$</big> | ||
となります。分子をデータの2乗のグループと\( \overline{x} \)のグループと\( \overline{x^2} \)のグループで整理すると | となります。分子をデータの2乗のグループと\( \overline{x} \)のグループと\( \overline{x^2} \)のグループで整理すると | ||
<big> | <big>$$ = \frac{ a^2+b^2+c^2+d^2+(-2a\overline{x})+(-2b\overline{x})+(-2c\overline{x})+(-2d\overline{x})+\overline{x}^2 +\overline{x}^2 +\overline{x}^2 +\overline{x}^2}{4} $$ </big> | ||
ここで、グループ毎に分数表記を分けます。 | ここで、グループ毎に分数表記を分けます。 | ||
<big> | <big>$$ = \frac{ a^2+b^2+c^2+d^2}{4}+\frac{(-2a\overline{x})+(-2b\overline{x})+(-2c\overline{x})+(-2d\overline{x})}{4}+\frac{\overline{x}^2 +\overline{x}^2 +\overline{x}^2 +\overline{x}^2}{4} $$</big> | ||
真ん中のグループはどれも−2倍されていますからこれを纏めます。分配法則の\( (ab+ac)=a(b+c) \)を利用します。最後のグループでは\( \overline{x}^2 \)を4回足すので4倍と同じことですので、表記を4倍で書き換えます。 | 真ん中のグループはどれも−2倍されていますからこれを纏めます。分配法則の\( (ab+ac)=a(b+c) \)を利用します。最後のグループでは\( \overline{x}^2 \)を4回足すので4倍と同じことですので、表記を4倍で書き換えます。 | ||
<big> | <big>$$ = \frac{ a^2+b^2+c^2+d^2}{4}+\frac{(-2)(a\overline{x}+b\overline{x}+c\overline{x}+d\overline{x})}{4}+\frac{4\overline{x}^2}{4} $$ </big> | ||
真ん中のグループはどれも\( \overline{x} \)倍されているのでこれも纏めます。括り出すとも言います。 | 真ん中のグループはどれも\( \overline{x} \)倍されているのでこれも纏めます。括り出すとも言います。 | ||
<big> | <big>$$ = \frac{a^2+b^2+c^2+d^2}{4}+\frac{(-2)\times\overline{x}(a+b+c+d)}{4}+\frac{4\overline{x}^2}{4} $$</big> | ||
真ん中のグループの分数部分の積の部分を外に出して書き方を少し変えます。わかりやすくする為です。 | 真ん中のグループの分数部分の積の部分を外に出して書き方を少し変えます。わかりやすくする為です。 | ||
<big> | <big>$$ = \frac{ a^2+b^2+c^2+d^2}{4}+(-2)\times\overline{x}\times\frac{a+b+c+d}{4}+\frac{4\overline{x}^2}{4} $$</big> | ||
そうすると真ん中のグループの分数部分はデータの平均と同じ形\( \overline{x} \)なので、書き換え、最後のグループは約分します。 | そうすると真ん中のグループの分数部分はデータの平均と同じ形\( \overline{x} \)なので、書き換え、最後のグループは約分します。 | ||
<big> | <big>$$ = \frac{a^2+b^2+c^2+d^2}{4}+(-2)\times\overline{x}\times\overline{x}+\frac{\cancel{4}\overline{x}^2}{\cancel{4}} $$</big> | ||
真ん中のグループは\( \overline{x} \)同志の積があるので、べき乗を使った表記にします。 | 真ん中のグループは\( \overline{x} \)同志の積があるので、べき乗を使った表記にします。 | ||
<big> | <big>$$ = \frac{ a^2+b^2+c^2+d^2}{4}+(-2\overline{x}^2)+\overline{x}^2 $$</big> | ||
一番最初のグループはデータを2乗したものの平均なので\( \overline{x^2} \)と表して、残った項目の整理をすると\( -2a+a=-a\)と同じような演算を適用して | 一番最初のグループはデータを2乗したものの平均なので\( \overline{x^2} \)と表して、残った項目の整理をすると\( -2a+a=-a\)と同じような演算を適用して | ||
<big> | <big>$$ = \overline{x^2}-\overline{x}^2 $$</big> | ||
これで分散が\( \overline{x^2}-\overline{x}^2 \)という演算でも求められることが確認出来ました。 | これで分散が\( \overline{x^2}-\overline{x}^2 \)という演算でも求められることが確認出来ました。 | ||
| 203行目: | 231行目: | ||
<big> | <big>$$\sigma^{2} = \int (x-\mu)^{2} \cdot f(x) \cdot dx $$ </big> | ||
\( (a - b)^2 = a^2 -2ab + b^2 \)のような計算を適用して展開すると | \( (a - b)^2 = a^2 -2ab + b^2 \)のような計算を適用して展開すると | ||
<big> | <big>$$ = \textcolor{red}{\int x^2 \cdot f(x) \cdot dx} - \textcolor{blue}{\int 2\mu x \cdot f(x) \cdot dx} + \textcolor{green}{\int \mu^{2} \cdot f(x) \cdot dx} $$ </big> | ||
上記のように整理できて1項<span style="color:red;"><span>(</span>赤<span>)</span></span>はデータを2乗した平均の形になっており、2項<span style="color:blue;"><span>(</span>青<span>)</span></span>は\(2\mu \times\)期待値の形、3項<span style="color:green;"><span>(</span>緑<span>)</span></span>は\( \int f(x) \cdot dx = 1 \)という確率密度関数の定義に従って\( \mu^2 \times 1 \)となります。従って、\( = E[ ] \)のEはExpected Valueを意味するEで、大文字のEに[]の中にかかれたデータの平均という意味の記号を用いて表現していくと、 | 上記のように整理できて1項<span style="color:red;"><span>(</span>赤<span>)</span></span>はデータを2乗した平均の形になっており、2項<span style="color:blue;"><span>(</span>青<span>)</span></span>は\(2\mu \times\)期待値の形、3項<span style="color:green;"><span>(</span>緑<span>)</span></span>は\( \int f(x) \cdot dx = 1 \)という確率密度関数の定義に従って\( \mu^2 \times 1 \)となります。従って、\( = E[ ] \)のEはExpected Valueを意味するEで、大文字のEに[]の中にかかれたデータの平均という意味の記号を用いて表現していくと、 | ||
<big> | <big>$$ = E[\mathrm{X}^2] - 2\mu \times \mu + \mu^2 $$ </big> | ||
となって、\( 2\mu \times \mu = 2\mu^2 \)と整理して | となって、\( 2\mu \times \mu = 2\mu^2 \)と整理して | ||
<big> | <big>$$ = E[\mathrm{X}^2] - 2 \mu^2 + \mu^2 $$ </big> | ||
で、以下のようになります。さらに\( \mu^2 \)の項同志を整理して | で、以下のようになります。さらに\( \mu^2 \)の項同志を整理して | ||
<big> | <big>$$ = E[\mathrm{X}^2] - \mu^2 $$</big> | ||
となって、平均値の2乗を期待値の2乗の表記に直すと以下のようになります。 | となって、平均値の2乗を期待値の2乗の表記に直すと以下のようになります。 | ||
<big> | <big>$$ = E[\mathrm{X}^2] - E[\mathrm{X}]^2 $$ </big> | ||
| 220行目: | 248行目: | ||
2乗したものの平均を確率密度関数から算出しようとすると | 2乗したものの平均を確率密度関数から算出しようとすると | ||
<big> | <big>$$ E[\text{X}] = \int x \cdot f(x) \cdot dx $$</big> | ||
で、データ\( x \)を確率密度関数にかけるとデータ\( x \)の平均値が算出できるので、\( x^2 \)を確率密度関数にかけるとデータ\( x^2 \)の平均値が算出できると言えます。そのことをグラフで確認したのが以下のグラフでプログラムで積分した値はデータを\( x^2 \)したときの平均値になっています。グラフは分散\( \sigma = 1 \)に固定しています。 | で、データ\( x \)を確率密度関数にかけるとデータ\( x \)の平均値が算出できるので、\( x^2 \)を確率密度関数にかけるとデータ\( x^2 \)の平均値が算出できると言えます。そのことをグラフで確認したのが以下のグラフでプログラムで積分した値はデータを\( x^2 \)したときの平均値になっています。グラフは分散\( \sigma = 1 \)に固定しています。 | ||
| 226行目: | 254行目: | ||
[[ファイル:Zsigma1NormalDistdz z-vs-z x z Mu 0 hatch Edit.png |650px | | |確率密度timesXvsX^2average0]] | [[ファイル:Zsigma1NormalDistdz z-vs-z x z Mu 0 hatch Edit.png |650px | | |確率密度timesXvsX^2average0]] | ||
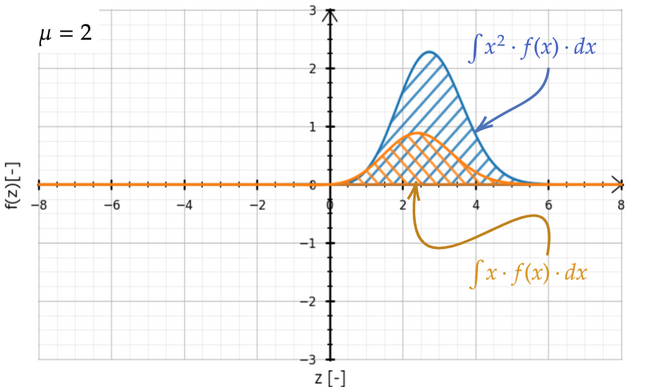
上記のように\( \mu = 0 \)のときは\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均しているため積分値も1になります。一方\( x \)をかけた方の黄色のグラフは奇関数になって積分値は0です。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 | 上記のように\( \mu = 0 \)のときは\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均しているため積分値も1になります。一方\( x \)をかけた方の黄色のグラフは奇関数になって積分値は0です。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 \)が分散を示す計算と同じで\( 1 - 0^2 \)で1になり、\( \sigma = 1 \)に固定していることが裏付けられます。 | ||
[[ファイル:Zsigma1NormalDistdz z-vs-z x z Mu 2 hatch fit edit.png |650px | | |確率密度timesXvsX^2average0]] | [[ファイル:Zsigma1NormalDistdz z-vs-z x z Mu 2 hatch fit edit.png |650px | | |確率密度timesXvsX^2average0]] | ||
上記のように\( \mu = 2 \)のときも同じように\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均していて積分値は5になります。平均値が2なので\( x \)をかけた方の黄色のグラフは積分値は2なっています。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 | 上記のように\( \mu = 2 \)のときも同じように\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均していて積分値は5になります。平均値が2なので\( x \)をかけた方の黄色のグラフは積分値は2なっています。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 \)が分散を示す計算と同じで\( 5 - 2^2 \)で1になり、\( \sigma = 1 \)に固定していることが裏付けられます。積分は実際にプログラムで計算させたないと実感できないかもしれません。 | ||
| 236行目: | 264行目: | ||
このことを利用してデータを2乗する\( \text{x}^2 \)の平均値\( E[\text{x}^2] \)は以下のように演算できます。 | このことを利用してデータを2乗する\( \text{x}^2 \)の平均値\( E[\text{x}^2] \)は以下のように演算できます。 | ||
<big> | <big>$$ E[\text{X}^2] = \int x^2 \cdot f(x) \cdot dx $$</big> | ||
注意したいのは、\( \int x \cdot f(x) \cdot dx \) \( x \)部分に\( x^2 \)を与えた訳ではなく、つまり\( x \)と\( f(x) \)の\( x \)に\( x^2 \)を代入した訳ではなく、確率密度関数に \( x \)を掛けた時に積分でデータ群\( X \)の期待値が求まることであり、確率密度関数の積分値は1で固定されている性質をもつ関数で確率密度関数にかけるものが\( x \)ならデータ群\( X \)の期待値、\( x^2 \)ならデータ群\( X^2 \)の期待値が求まる。つまりデータ\( x \)を2乗した期待値を求められる事です。ですから以下のように\( x^2 \)を掛けると | 注意したいのは、\( \int x \cdot f(x) \cdot dx \) \( x \)部分に\( x^2 \)を与えた訳ではなく、つまり\( x \)と\( f(x) \)の\( x \)に\( x^2 \)を代入した訳ではなく、確率密度関数に \( x \)を掛けた時に積分でデータ群\( X \)の期待値が求まることであり、確率密度関数の積分値は1で固定されている性質をもつ関数で確率密度関数にかけるものが\( x \)ならデータ群\( X \)の期待値、\( x^2 \)ならデータ群\( X^2 \)の期待値が求まる。つまりデータ\( x \)を2乗した期待値を求められる事です。ですから以下のように\( x^2 \)を掛けると | ||
<big> | <big>$$ = \int x^2 \cdot \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{1}{2\sigma^2}(x-\mu)^2} \cdot dx $$</big> | ||
ここで、先の期待値の確認でもやったように\( z = \frac{x -\mu}{\sigma} \)…<span>(</span>2<span>)</span>という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… <span>(</span>3<span>)</span>で、 <span>(</span>2<span>)</span>および<span>(</span>3<span>)</span>の式を当てはめると | ここで、先の期待値の確認でもやったように\( z = \frac{x -\mu}{\sigma} \)…<span>(</span>2<span>)</span>という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… <span>(</span>3<span>)</span>で、 <span>(</span>2<span>)</span>および<span>(</span>3<span>)</span>の式を当てはめると | ||
<big>\($ \int^{\infty}_{-\infty}\textcolor{red}{x^2(←(3)式)} \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\textcolor{blue}{\sigma^{2}}}\textcolor{blue}{(x-\mu)^{2}(←(2)式)}}\cdot dx $\)</big> | <big>\($ \int^{\infty}_{-\infty}\textcolor{red}{x^2(←(3)式)} \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\textcolor{blue}{\sigma^{2}}}\textcolor{blue}{(x-\mu)^{2}(←(2)式)}}\cdot dx $\)</big> | ||
を上記のように適用します。以降σに斜線が入っているところは置換積分の正しい手順のやり忘れの間違いでした。後で気付いたので、残しておこうと思います。後ほど解説もあります。うっかりうっかりです。知能不足である管理人<span>(</span>自分<span>)</span>の証拠の証拠として残しました。それで計算を進めると | を上記のように適用します。以降σに斜線が入っているところは置換積分の正しい手順のやり忘れの間違いでした。後で気付いたので、残しておこうと思います。後ほど解説もあります。うっかりうっかりです。知能不足である管理人<span>(</span>自分<span>)</span>の証拠の証拠として残しました。それで計算を進めると | ||
<big> | <big>$$ \int^{\infty}_{-\infty} \textcolor{red}{(z \cdot \sigma + \mu)^2 } \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$</big> | ||
となって、<span>(</span>3<span>)</span>式の部分を\( (a+b)^2 = a^2+2ab+b^2 \)を適用して、 | となって、<span>(</span>3<span>)</span>式の部分を\( (a+b)^2 = a^2+2ab+b^2 \)を適用して、 | ||
<big> | <big>$$ \int^{\infty}_{-\infty} \textcolor{red}{(z^2 \cdot \sigma^2 + 2z\cdot \sigma \cdot \mu + \mu^2) } \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$</big> | ||
となります。<span>(</span>2<span>)</span>式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して | となります。<span>(</span>2<span>)</span>式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して | ||
<big> | <big>$$ \int^{\infty}_{-\infty} z^2 \cdot \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz+ \int^{\infty}_{-\infty} 2z\cdot \sigma \cdot \mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz + \int^{\infty}_{-\infty} \mu^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
定数倍部分を積分の外に出しても問題ないので外に出した表記にしてみます。 | 定数倍部分を積分の外に出しても問題ないので外に出した表記にしてみます。 | ||
<big> | <big>$$ \sigma^2 \cdot \int^{\infty}_{-\infty} z^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 2\sigma\mu \cdot \int^{\infty}_{-\infty}z \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz + \mu^2 \cdot \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
真ん中の項は先の平均値の算出でやったとおり奇関数なので積分をすると0です。一番後ろの項は積分の部分が確率密度関数そのものなので1になります。\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。で、一番最初の項目がどうなるかを考えないといけないです。まずは整理したものを以下に記述すると | 真ん中の項は先の平均値の算出でやったとおり奇関数なので積分をすると0です。一番後ろの項は積分の部分が確率密度関数そのものなので1になります。\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。で、一番最初の項目がどうなるかを考えないといけないです。まずは整理したものを以下に記述すると | ||
<big> | <big>$$ \sigma^2 \cdot \int^{\infty}_{-\infty} z^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 2\sigma\mu \cdot 0 + \mu^2 \cdot 1 $$</big> | ||
<big> | <big>$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot \int^{\infty}_{-\infty} z^2 \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 0 + \mu^2 $$</big> | ||
部分積分の公式を使って | 部分積分の公式を使って | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big | | style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> $$ \int f(x) \cdot g^{\prime}(x) \cdot dx = f(x) \cdot g(x) - \int f^{\prime}(x) \cdot g(x) \cdot dx $$</big> | ||
|} | |} | ||
<big> | <big>$$ ( \textcolor{red}{e^{- \frac{z^2}{2}}})^{\prime} = \textcolor{blue}{-z \cdot e^{-\frac{z^2}{2}}} $$</big> | ||
なので、 | なので、 | ||
<big> | <big> $$ \int^{\infty}_{-\infty} z^2 \cdot e^{-\frac{z^{2}}{2}}\cdot dz = \int^{\infty}_{-\infty} \textcolor{green}{-z} \cdot \textcolor{blue}{(e^{- \frac{z^2}{2}})^{\prime}} \cdot dz $$</big> | ||
ですから、 | ですから、 | ||
<big> | <big> $$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} - \int^{\infty}_{-\infty} (\textcolor{green}{-z})^{\prime} \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$</big> | ||
となって | となって | ||
<big> | <big> $$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} - \int^{\infty}_{-\infty} \textcolor{green}{-1} \cdot \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$</big> | ||
上記の−1を整理して | 上記の−1を整理して | ||
<big> | <big> $$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} + \int^{\infty}_{-\infty} \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$</big> | ||
<big> | <big>$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot (\left[ -z e^{-\frac{z^{2}}{2}} \right]^{\infty}_{-\infty}+ \int^{\infty}_{-\infty} e^{-\frac{z^{2}}{2}} \cdot dz) + 0 + \mu^2 $$</big> | ||
<big> | <big>$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot (0 + \sqrt{2\pi}) + 0 + \mu^2 $$</big> | ||
あれ? | あれ? | ||
<big> | <big>$$ \sigma^2 + 0 + \mu^2 $$</big> | ||
になるはずでこれに\( \textcolor{red}{ E[\mathrm{X}^2]} \textcolor{black}{- E[\mathrm{X}]^2 =} \textcolor{red}{(\sigma^2+\mu^2)} \textcolor{black}{ - \mu^2 = \sigma^2} \)となる予定だったんすけど | になるはずでこれに\( \textcolor{red}{ E[\mathrm{X}^2]} \textcolor{black}{- E[\mathrm{X}]^2 =} \textcolor{red}{(\sigma^2+\mu^2)} \textcolor{black}{ - \mu^2 = \sigma^2} \)となる予定だったんすけど \( \sqrt{2\pi}\sigma \)でσが一個、分母に余計に残った。おかしいなと思って他のサイト見てみたら他のサイトではしれっとσが消えてるとこもありました。神戸大学の人の文献のようです。神戸大学の人の文献では自信をもってσが分母から消えているので、計算は合っているのかもしれないが、自分のわからない理論で消えているのは確かだ。わからない。困った。こんなん考えてるの自分らくらいなので、なかなか自分の計算を助けてくれる文献には出会えない。残念だけど、暫く保留だな。所詮は放送大学卒の頭脳ってことだな。解ける人は解いてみて下さい。[http://www.math.kobe-u.ac.jp/HOME/higuchi/ 神戸大学 樋口教授のノート] > > >平成24年度後期の講義ノート<span>(</span>notes for 2012 autumn<span>)</span> > > > 確率論1 <span>(</span> Probability 1 <span>)</span>, 微分積分学2 <span>(</span> bibun-sekibun-gaku <span>)</span> > > >[http://www.math.kobe-u.ac.jp/HOME/higuchi/h24kogi/12prob1-5.pdf 11月2日講義ノート] の3ページ目から4ページ目にまたがるところが、自分の謎な部分。 | ||
しゅん…。 | しゅん…。 | ||
| 289行目: | 317行目: | ||
置換積分の公式は | 置換積分の公式は | ||
{| style = "width: 100%;" | {| style = "width: 100%;" | ||
| style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> | | style= "font-weight: bold; background-color: #f2f6ff; white-space:nowrap; padding:10px; border: dotted 1px black; border-radius: 10px;" | <big> $$ x=g(t) $$ <span style="font-size: smaller; font-weight: normal;">とおくと、</span> $$\int f(x) \cdot dx= \int f(g(t))\frac{dx}{dt}\cdot dt $$</big> | ||
|} | |} | ||
公式をきちんと適用すると具体的には、 | 公式をきちんと適用すると具体的には、 | ||
<big> | <big>$$ x = \sigma \cdot z + \mu $$</big> | ||
とおいているので | とおいているので | ||
<big> | <big>$$ \frac{dx}{dz} $$</big> | ||
は | は | ||
<big> | <big>$$ \sigma \cdot z + \mu $$</big> | ||
というxの式をzで微分するという意味で、 | というxの式をzで微分するという意味で、 | ||
<big> | <big>$$ \frac{dx}{dz} = \sigma $$</big> | ||
になるので、zで置換した積分の式に\( \frac{dx}{dz}\)を掛けるのが置換積分ですから、以下のようになります。 | になるので、zで置換した積分の式に\( \frac{dx}{dz}\)を掛けるのが置換積分ですから、以下のようになります。 | ||
<big> | <big>$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\sigma} \cdot \textcolor{red}{ \sigma } \textcolor{black}{ \cdot \int^{\infty}_{-\infty}-z e^{-\frac{z^{2}}{2}}\cdot dz } $$</big> | ||
なので、 | なので、 | ||
<big> | <big>$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}} \cdot (\int^{\infty}_{-\infty}-z e^{-\frac{z^{2}}{2}}\cdot dz $$</big> | ||
となります。 | となります。 | ||
だから、σが分母に残っていたのは無くなって | だから、σが分母に残っていたのは無くなって | ||
<big> | <big>$$ \sigma^2 + 0 + \mu^2 $$</big> | ||
になります。なので、 | になります。なので、 | ||
<big> | <big>$$ E[\mathrm{X^2}] = \sigma^2 + 0 + \mu^2 $$</big> | ||
ですから、分散\( V[X] = \textcolor{red}{ E[\mathrm{X^2}] } - \textcolor{blue}{ E[\mathrm{X}]^2 } \)VはVarianceのVで、これは | ですから、分散\( V[X] = \textcolor{red}{ E[\mathrm{X^2}] } - \textcolor{blue}{ E[\mathrm{X}]^2 } \)VはVarianceのVで、これは | ||
<big> | <big>$$ V[X] = \textcolor{red}{ \sigma^2 + 0 + \mu^2 } \textcolor{black}{-} \textcolor{blue}{\mu^2} $$</big> | ||
<big> | <big>$$ V[X] = \sigma^2 $$</big> | ||
となるので、 | となるので、 | ||
<big> | <big>$$ \sigma^2 = \int (x - \mu)^2 \cdot f(x) \cdot dx $$</big> | ||
であることが確認できたことになります。 | であることが確認できたことになります。 | ||
| 325行目: | 353行目: | ||
確率密度関数はこうなんじゃないか?という随分前のところで | 確率密度関数はこうなんじゃないか?という随分前のところで | ||
<big> | <big> $$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}} e^{-\mathrm{N}(x-\mu)^2} \cdot dx = 1 $$ </big> | ||
まで求めてました。積分して1になるちょうど良い膨らみの係数を求めることです。 | まで求めてました。積分して1になるちょうど良い膨らみの係数を求めることです。 | ||
2023年2月25日 (土) 15:57時点における最新版
Pythonの記事へ戻る
記事作成途中で、今のところ、何がPythonなの?っていう記事になっています。Python要素ゼロです。管理人はグラフを書くのにちょくちょく使ってますが、グラフを書く説明以上に統計的な知識を微分積分もあまりよくわからない人向けに難しい式変形を落とし込むという作業で管理人自身が苦しんでいます。意外とわかっていなかったことってあるんだなぁ。と、そのように思っていて、人に教えるような資格はないのではないかと感じ始めています。でも、まぁ頑張ってみます。いろんなサイトを検索したけど、ここまで真面目に向き合っているサイトは検索しても検索しても出てこないので、この記事が出来上がったら、確率・統計が手に取るようにわかるようになると思います。統計を制するもの製造を制する。世界を制する。ありとあらゆる現象を制するのだと思うと、有用なものになるんではないか。そう信じて、歩き続ける。
正規分布の公式
■正規分布の確率密度を算出する式の作り方
作りたい関数の方針〜求めるべき係数
確率密度関数は以下のように定義されます.。
| $$ f( x) \ =\ \frac{1}{\sqrt{2\pi } \sigma }\exp^{-\frac{1}{2\sigma } (x-\mu )^{2}} $$ |
この項目ではこの確率密度関数をpythonを使いつつ理解しようとすることを目指します。
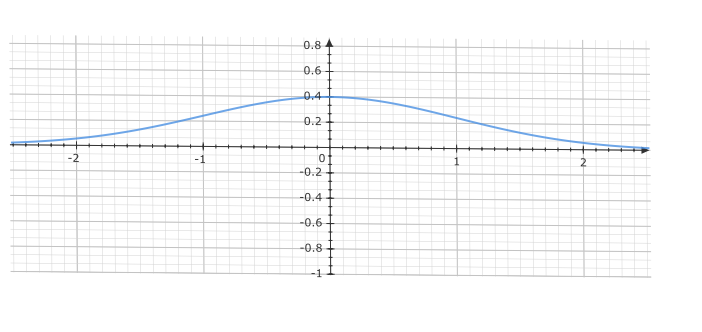
確率密度の関数は以下のようなグラフになるような関数であるべきで、
1.\( f( x) = -x^{2} \)のような上に凸になるようにする。
2.両端で限りなく0に近づくようにすること。
3.\( \int ^{\infty }_{-\infty } f( x) \)で積分すると1(グラフで言うと関数の描く曲線がy=0の線と囲まれているところの面積が1ということ)になる。
Python_matplotlibで学ぶ…グラフ描画プログラム
上記のようなことをみたす関数を考えると\( a^{-x^{2}} \)のような関数であれば急激に0に近づく関数として適切であることが、予想できます。例えば\( a = 2 \)と固定してみた場合\( x \)が\( -4, -3, -2, -1, 0, 1, 2, 3, 4, \)…のように変化すると、\( 2^{-(16=(-4)*(-4))}=\frac{1}{2^{16}}, 2^{-9}=\frac{1}{2^{9}}, 2^{-4}=\frac{1}{2^{4}}, 2^{-1}=\frac{1}{2^{1}}, 2^{0}=1, 2^{-1}=\frac{1}{2^{1}}, 2^{-4}=\frac{1}{2^{4}}, 2^{-9}=\frac{1}{2^{9}}, 2^{-16}=\frac{1}{2^{16}} \)となることから予想は概ね正しいと言えることが分かってもらえると思います。
簡単な予想で形だけは近いグラフになる関数になりましたが、まだ積分が1になるようなグラフにはなっていないかもしれないです。グラフの山の高さと広がり方を調整しないと積分して1になる正規分布の確率密度を表すようなグラフを描いたことにはならないです。もう少し工夫が必要です。
というわけで、さらに積分して1にする必要があるため、積分が簡単なように冪乗の底となる\( a \)を積分しやすいように考えられたネイピア数\( e \)を底とするために、\( a = e^{\log_e a} \)のような式を使うことを考えるようにしてみます。これは\( e \)を\( a \)乗したら\( a \)になるような関係を示しているだけです。対数の\( \mathrm{N} = \log_e a \)は\( e^{\mathrm{N}} = a \)を\( \log \)という表記方法にしたものです。対数は積の計算を和に還元するためにあります。\( x^{a}x^{b} = x^{a+b} \)といったような指数法則を利用するものです。この時の\( x \)を底と呼んでいて、対数的な考え方においては底という数字はなんでもいいのです。対数表のようなものから計算ができれば、巨大な積を和に還元できるからです。なので\( \log_e \)のような複雑そうな底を使うことが基本になっています。\( \log_{e} \)の\( e \)を省略した\( \log \)も\( \log_{e} \)と同じものを表すことになっています。ネイピア数\( e \)を対数の底にするのは実は複雑そうで意外と綺麗にまとまる値だからです。ちまちました計算で頭で理解しながら対数の仕組み確かめたい場合は常用対数のような\( \log_{10} \)とかを使うのでしょう。でもそれは対数の仕組みを理解することが主な利用用途であることが多いです。一部常用対数で桁数を求めたりする用途もありますが、本来は\( \log_{e} \)のような自然対数を使うことの方が、微分積分を多様する自然科学においての主な使い方になります。
\( a^{-x^{2}} = e^{-\log_ea x^{2}} \)の\( \mathrm{N} = \log_ea \)とおくと\( a^{-x^{2}} = e^{-\mathrm{N} x^{2}} \)
上記のような表現をした時の\( \mathrm{N} \)を究明することが確率密度関数を見つけることになります。
ところで、
| $$ \int e^{-x^2} \cdot dx = \sqrt{\pi}$$ |
ということが分かっていて、
| $$ \int e^{-\mathrm{N}x^2} \cdot dx = \sqrt{\frac{\mathstrut\pi}{\mathstrut \mathrm{N}}} \tag{1} $$ |
となります。と言っても本当にそうなのかということもありますので、
ネイピア数のマイナスx乗の2乗の積分の記事にて、その証明を記載します。後でなりますが…今のところは積分の公式だと思ってください。この公式も掘り下げて考え始めると加減乗除くらいしか出来ない人からすると、理解するのに3時間はかかると思います。
さてさて、証明を理解したとして、\( (1) \)の式の両辺に\( \sqrt{\frac{\mathrm{N}}{\pi}} \)を掛けて
$$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut\pi}} e^{-\mathrm{N}x^2} \cdot dx = \sqrt{\frac{\mathstrut\pi}{\mathstrut \mathrm{N}}}\sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}}= 1 $$
\( x \)のデータから平均値\( \mu \)分を引いて\( x \)軸の0を中心にデータが分散するような式に変換するため\( x \)を\( x - \mu \)に置き換えて置きます。
$$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}} e^{-\mathrm{N}(x-\mu)^2} \cdot dx = 1 $$
求めるべき係数の算出の前に〜確率密度関数から考える期待値・平均値と分散値について
ここで、確率密度の関数の積分と確率密度関数と平均値(期待値)、分散の関係を纏めておきます。平均値と期待値はよく似ている表現ですが、期待値にはゆくゆくはそうなるだろうという収束する着地点を表し、平均値は過去の実際のデータが示す値をひらたくした値という意味合いが強いです。ここでは厳密な使い分けをせず使っています。え?こういう時って平均値じゃなくて期待値って単語をつかうんじゃね?とか、そういうのは本来の意味を理解した上で個々人で変換して下さい。こちらとして、どっちかの意味であるかを厳密にする必要がある場合は単語を使う前にことわりを入れます。え?それって間違った表現もしますって宣言しているんじゃね?とか思ったでしょう。そういうことです。でも時々、意味は違うんで意識します。くらいの感じです。え?それってやばくね。このページの正確さやばくね?まぁね。やばいね。でもね。気楽に考えようって事もあるんですよ。だってどういう題材を扱っているかは人の気持ち次第だし。全部のデータがそろっていて、そのことについて言っているのか、まだそろっていないこれからのことを含めて考えているのかなんてのは、その時の考え方次第だし、人それぞれ自由だと思うんです。
| 累積確率密度 $$ 1 = \int f(x) \cdot dx $$ 平均値 $$\mu = \int x \cdot f(x) \cdot dx $$ 分散 $$\sigma^{2} = \int (x-\mu)^{2} \cdot f(x) \cdot dx $$ |
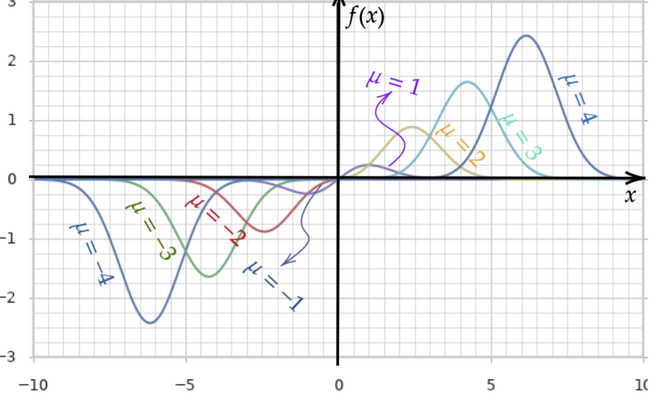
確率密度関数の積分で表現する平均値は以下のようなグラフになります。
確率密度関数で積分して1となる面積にデータである\( x \)を掛ければ面積が平均値と一致します。確率密度の関数のパラメータの\( \sigma \)を\( 1 \)に固定すれば、上記のグラフのように\( \mu \)がプラスの時は上側にコブが出来るグラフでマイナスのときは下側にコブが出来るグラフになります。もちろん面積は\( \mu \)と同じ値になります。\( \mu \)が大きいほど大きいコブになって面積が大きくなっていきます。マイナス側も同じで小さくなるほど、コブが下向きで大きくなってマイナスの面積が大きくなります。\( \mu \)が\( 0 \)のときだけ、\( f(x)=-x \)のグラフで対称となる小さなコブができた状態でプラス側では上向きにマイナス側では下向きにコブができます。面積合計は打ち消しあって0になります。なんで、正規分布の積分をする前の\( f(x) \)に対して\( x \)をかけてから積分すると、これほど都合よく平均値と一致させることができるのか?確かめる必要があります。では少し確認してみることにしましょう。
$$ \int^{\infty}_{-\infty} f(x)\cdot dx = \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$
のような形式が正規分布の関数で、一番最初に示した求めるべき結果でした。まだ証明していないのに利用するのはずるいですが、これに\( x \)をかけると
$$ \int^{\infty}_{-\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$
上記の式が平均値を求める式で、それってあってるの?という探究の始まりした。ここで、\( z = \frac{x -\mu}{\sigma} \)…(2)という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… (3)で、 (2)および(3)の式を当てはめると
$$ \int^{\infty}_{-\infty}\textcolor{red}{x(←(3)式)} \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\textcolor{blue}{\sigma^{2}}}\textcolor{blue}{(x-\mu)^{2}(←(2)式)}}\cdot dx $$
を上記のように適用すると
$$ \int^{\infty}_{-\infty} (\textcolor{red}{z \cdot \sigma + \mu}) \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$
となります。\( \sigma \)に斜線が入っているのは後で置換積分の間違いに気付いたもので、あえて記録を残しています。後ほど細かい説明をしています。 (2)式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して
$$ \textcolor{green}{\int^{\infty}_{-\infty} z \cdot \sigma \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz} + \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi} \cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$
上記のようになり、2つの積分の和の構造の最初の積分の部分(緑)はちょっと確かめれば原点を通過する奇関数と呼ばれる形式になっています。要するに積分をすると0になるということです。グラフをプロットして確かめてみると以下の通りです。
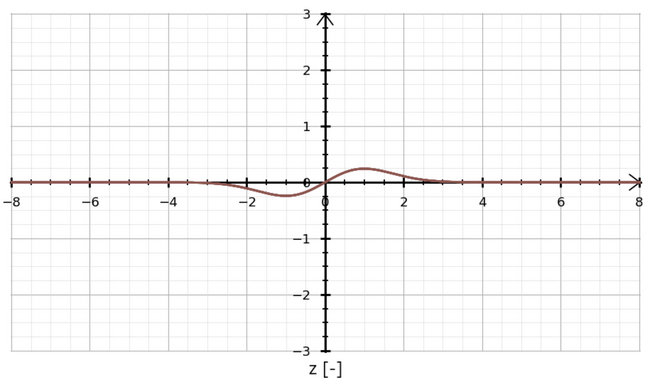 $$ 0 + \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$
と、上記のように定数\( \mu \)倍を使って積分する式になります。そうすると上記の式から\( \mu \)を除いた部分
$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$
は確率密度関数で積分(グラフのプロットとy=0に囲まれた部分面積を求める操作でマイナス領域とプラス領域の差し引きをする)をすると1になるものですから、最終的には
$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz = 1 $$
で、先程示された式は定数\( \mu \)倍を使って積分する式\( \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz \)と表現することができます。確率密度関数の中の\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。
\($ \mu \cdot 1 $\)
となりますから、元々の式の計算結果は平均値を意味する\( \mu \)であると言えます。確率密度関数\( f(x) \)を\( x \)倍したものの積分は\( \mu \)になることが確認でき、
$$ \mu = \int^{\infty}_{-\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$
$$\mu = \int x \cdot f(x) \cdot dx $$
であると言えます。
$$ 0 + \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$
と、上記のように定数\( \mu \)倍を使って積分する式になります。そうすると上記の式から\( \mu \)を除いた部分
$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$
は確率密度関数で積分(グラフのプロットとy=0に囲まれた部分面積を求める操作でマイナス領域とプラス領域の差し引きをする)をすると1になるものですから、最終的には
$$ \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz = 1 $$
で、先程示された式は定数\( \mu \)倍を使って積分する式\( \int^{\infty}_{-\infty}\mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz \)と表現することができます。確率密度関数の中の\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。
\($ \mu \cdot 1 $\)
となりますから、元々の式の計算結果は平均値を意味する\( \mu \)であると言えます。確率密度関数\( f(x) \)を\( x \)倍したものの積分は\( \mu \)になることが確認でき、
$$ \mu = \int^{\infty}_{-\infty} x \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}\cdot dx $$
$$\mu = \int x \cdot f(x) \cdot dx $$
であると言えます。
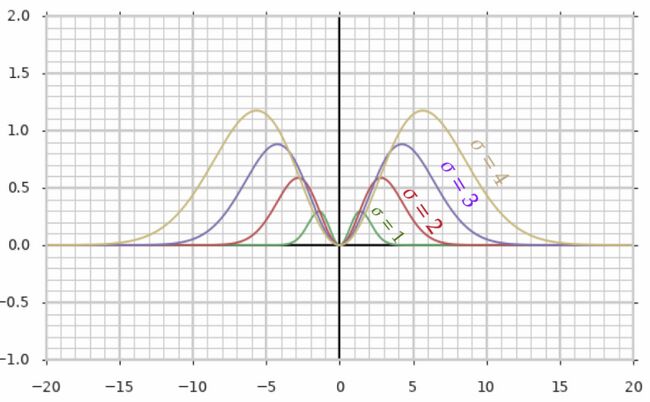
確率密度関数の積分で表現する分散値は以下のようなグラフになります。
確率密度関数で積分して1だった面積に分散値である\( (x - \mu)^2 \)を掛ければ面積が分散値と一致します。そのようになるようにした関数のグラフは平均値\( \mu \)を\( 0 \)とすると上記のように\( x = 0 \)の軸で鏡になったようなコブが二つプラス側で並びます。分散値は個別のデータ\( x \)を平均値\( \mu \)との差をとって2乗した値なので必ずプラスになるためです。分散値が大きいほどコブは大きくなり面積が多くなることもグラフから確認できます。確率密度関数から表現できる積分して分散値になるような関数とは上記のような形であることをイメージして置くと理解しやすい関数に思えるでしょう。このように要所要所で関数をグラフ化してイメージできるようにすることが理解を深めますので、コンピュータで関数のグラフを描いたり、積分値の近似できるプログラムから算出できるような技術力を持っていると学習の助けになるので、是非、少しづつ習得していって欲しいです。コンピュータに演算させれば、このグラフのそれぞれの関数の曲線と\( y = 0 \)の軸とで囲われた部分の面積は分散値になることも確認できます。関数の\( \mu \)を変化させるとコブのグラフ全体が\( \mu \)分だけ横にシフトします。面積が丁度半分になるところが平均値ですので、二つのコブの真ん中が\( y = 0 \)の点と接する部分の\( x \)の値が平均値に相当することになります。
とイメージだけでは怪しいので、確率密度関数に\( (x - \mu)^2 \)をかけたモノを積分するだけで分散が求まるのか、ここでも確認をしてみたいと思います。分散はデータを2乗したものの平均から平均値を2乗したものを引く \( \sigma^2=\overline{\text{x}^{2}} -\overline{\text{x}}^{2} \) で求めることができます。本当にそれでも分散が算出できるのかについても触れないといけないですね。ここで\( \overline{\text{x}} \)は全部のデータ\( \text{x} \)に対するの平均を意味します。オーバーラインの下にあるモノに対しての平均になります。\( x \)は一つのデータで、与えられた\( x \)は分布関数\( f(x) \)の値によって表現される全体のデータ出現頻度に相当する数値となり、\( x \)のときの\( f(x) \)で囲われる面積によって確率が決定されるものなのでした。このことを踏まえて、説明を続けます。
\( \sigma^2=\overline{\text{x}^{2}} -\overline{\text{x}}^{2} \)が成り立つことについての確認として、4つのデータ\( x =\)個別のデータ変数\({a,b,c,d} \)においては
$$ xの平均値 \overline{x} = \frac{ \mathrm{a}+b+c+d}{4} $$
個別のデータを2乗したものを平均化する
$$
\begin{align}
x^2の平均値 \overline{x^2} = \frac{\unicode{x0061}^2+b ^2 +c ^2 +d ^2}{4} \nonumber
\end{align}
$$
分散は個別のデータと平均値を引いたモノについて2乗して、それぞれ和にしたものをデータ数で割ったモノと定義されていますから、
$$ xの分散 \sigma^2 = \frac{(a-\overline{x})^2+ (b-\overline{x})^2 + (c-\overline{x})^2 + (d-\overline{x})^2}{4} $$
となって、上記の2乗になっている部分を展開すると分配法則の\( (a + b)^2 = a^2 + 2ab + b^2 \)を利用して
$$ = \frac{( a^2-2a\overline{x}+\overline{x}^2) + (b^2-2b\overline{x}+\overline{x}^2) + (c^2-2c\overline{x}+\overline{x}^2) + (d^2-2d\overline{x}+\overline{x}^2)}{4} $$
となります。分子をデータの2乗のグループと\( \overline{x} \)のグループと\( \overline{x^2} \)のグループで整理すると
$$ = \frac{ a^2+b^2+c^2+d^2+(-2a\overline{x})+(-2b\overline{x})+(-2c\overline{x})+(-2d\overline{x})+\overline{x}^2 +\overline{x}^2 +\overline{x}^2 +\overline{x}^2}{4} $$
ここで、グループ毎に分数表記を分けます。
$$ = \frac{ a^2+b^2+c^2+d^2}{4}+\frac{(-2a\overline{x})+(-2b\overline{x})+(-2c\overline{x})+(-2d\overline{x})}{4}+\frac{\overline{x}^2 +\overline{x}^2 +\overline{x}^2 +\overline{x}^2}{4} $$
真ん中のグループはどれも−2倍されていますからこれを纏めます。分配法則の\( (ab+ac)=a(b+c) \)を利用します。最後のグループでは\( \overline{x}^2 \)を4回足すので4倍と同じことですので、表記を4倍で書き換えます。
$$ = \frac{ a^2+b^2+c^2+d^2}{4}+\frac{(-2)(a\overline{x}+b\overline{x}+c\overline{x}+d\overline{x})}{4}+\frac{4\overline{x}^2}{4} $$
真ん中のグループはどれも\( \overline{x} \)倍されているのでこれも纏めます。括り出すとも言います。
$$ = \frac{a^2+b^2+c^2+d^2}{4}+\frac{(-2)\times\overline{x}(a+b+c+d)}{4}+\frac{4\overline{x}^2}{4} $$
真ん中のグループの分数部分の積の部分を外に出して書き方を少し変えます。わかりやすくする為です。
$$ = \frac{ a^2+b^2+c^2+d^2}{4}+(-2)\times\overline{x}\times\frac{a+b+c+d}{4}+\frac{4\overline{x}^2}{4} $$
そうすると真ん中のグループの分数部分はデータの平均と同じ形\( \overline{x} \)なので、書き換え、最後のグループは約分します。
$$ = \frac{a^2+b^2+c^2+d^2}{4}+(-2)\times\overline{x}\times\overline{x}+\frac{\cancel{4}\overline{x}^2}{\cancel{4}} $$
真ん中のグループは\( \overline{x} \)同志の積があるので、べき乗を使った表記にします。
$$ = \frac{ a^2+b^2+c^2+d^2}{4}+(-2\overline{x}^2)+\overline{x}^2 $$
一番最初のグループはデータを2乗したものの平均なので\( \overline{x^2} \)と表して、残った項目の整理をすると\( -2a+a=-a\)と同じような演算を適用して
$$ = \overline{x^2}-\overline{x}^2 $$
これで分散が\( \overline{x^2}-\overline{x}^2 \)という演算でも求められることが確認出来ました。
ここまで来たら疲れたよ。なんだか眠いんだよ状態ですが、本題にもどって、確率密度関数で表す分散値について追求しなおしましょう。
$$\sigma^{2} = \int (x-\mu)^{2} \cdot f(x) \cdot dx $$
\( (a - b)^2 = a^2 -2ab + b^2 \)のような計算を適用して展開すると
$$ = \textcolor{red}{\int x^2 \cdot f(x) \cdot dx} - \textcolor{blue}{\int 2\mu x \cdot f(x) \cdot dx} + \textcolor{green}{\int \mu^{2} \cdot f(x) \cdot dx} $$
上記のように整理できて1項(赤)はデータを2乗した平均の形になっており、2項(青)は\(2\mu \times\)期待値の形、3項(緑)は\( \int f(x) \cdot dx = 1 \)という確率密度関数の定義に従って\( \mu^2 \times 1 \)となります。従って、\( = E[ ] \)のEはExpected Valueを意味するEで、大文字のEに[]の中にかかれたデータの平均という意味の記号を用いて表現していくと、
$$ = E[\mathrm{X}^2] - 2\mu \times \mu + \mu^2 $$
となって、\( 2\mu \times \mu = 2\mu^2 \)と整理して
$$ = E[\mathrm{X}^2] - 2 \mu^2 + \mu^2 $$
で、以下のようになります。さらに\( \mu^2 \)の項同志を整理して
$$ = E[\mathrm{X}^2] - \mu^2 $$
となって、平均値の2乗を期待値の2乗の表記に直すと以下のようになります。
$$ = E[\mathrm{X}^2] - E[\mathrm{X}]^2 $$
という具合に分散の確率密度の式は紐解くとデータの2乗の平均と平均値の2乗の差のカタチになっていて、式は正しいです。ですが、さらにデータの2乗の平均の部分を確率密度関数を紐解いてみます。要するにデータを2乗したものの平均値と平均値の2乗がわかれば、その差によって分散値が求まるのですから
2乗したものの平均を確率密度関数から算出しようとすると
$$ E[\text{X}] = \int x \cdot f(x) \cdot dx $$
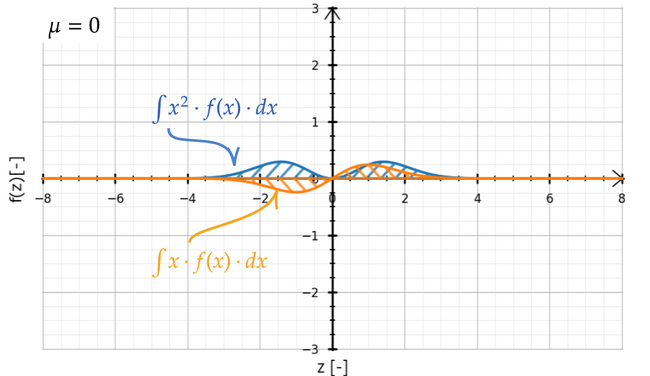
で、データ\( x \)を確率密度関数にかけるとデータ\( x \)の平均値が算出できるので、\( x^2 \)を確率密度関数にかけるとデータ\( x^2 \)の平均値が算出できると言えます。そのことをグラフで確認したのが以下のグラフでプログラムで積分した値はデータを\( x^2 \)したときの平均値になっています。グラフは分散\( \sigma = 1 \)に固定しています。
上記のように\( \mu = 0 \)のときは\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均しているため積分値も1になります。一方\( x \)をかけた方の黄色のグラフは奇関数になって積分値は0です。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 \)が分散を示す計算と同じで\( 1 - 0^2 \)で1になり、\( \sigma = 1 \)に固定していることが裏付けられます。
上記のように\( \mu = 2 \)のときも同じように\( x^2 \)をかけた方の青色のグラフは両側がプラスになってデータを2乗して平均していて積分値は5になります。平均値が2なので\( x \)をかけた方の黄色のグラフは積分値は2なっています。両方の積分値の差分をとることは\( E[\mathrm{X}^2] - E[\mathrm{X}]^2 \)が分散を示す計算と同じで\( 5 - 2^2 \)で1になり、\( \sigma = 1 \)に固定していることが裏付けられます。積分は実際にプログラムで計算させたないと実感できないかもしれません。
このことを利用してデータを2乗する\( \text{x}^2 \)の平均値\( E[\text{x}^2] \)は以下のように演算できます。
$$ E[\text{X}^2] = \int x^2 \cdot f(x) \cdot dx $$
注意したいのは、\( \int x \cdot f(x) \cdot dx \) \( x \)部分に\( x^2 \)を与えた訳ではなく、つまり\( x \)と\( f(x) \)の\( x \)に\( x^2 \)を代入した訳ではなく、確率密度関数に \( x \)を掛けた時に積分でデータ群\( X \)の期待値が求まることであり、確率密度関数の積分値は1で固定されている性質をもつ関数で確率密度関数にかけるものが\( x \)ならデータ群\( X \)の期待値、\( x^2 \)ならデータ群\( X^2 \)の期待値が求まる。つまりデータ\( x \)を2乗した期待値を求められる事です。ですから以下のように\( x^2 \)を掛けると
$$ = \int x^2 \cdot \frac{1}{\sqrt{2\pi}\sigma}\exp^{-\frac{1}{2\sigma^2}(x-\mu)^2} \cdot dx $$
ここで、先の期待値の確認でもやったように\( z = \frac{x -\mu}{\sigma} \)…(2)という\( z \)に置き換える式と、この式の両辺に\( \sigma \)をかけて\( z \cdot \sigma= \frac{x -\mu}{\sigma} \cdot \sigma \)、なので右辺の分母分子の\( \sigma \)を約分できて1になるから\( z \cdot \sigma= x -\mu \)となり、両辺に\( \mu \)を足して\( z \cdot \sigma + \mu = x \)つまり\( x = z \cdot \sigma + \mu \)… (3)で、 (2)および(3)の式を当てはめると \($ \int^{\infty}_{-\infty}\textcolor{red}{x^2(←(3)式)} \cdot \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2\textcolor{blue}{\sigma^{2}}}\textcolor{blue}{(x-\mu)^{2}(←(2)式)}}\cdot dx $\) を上記のように適用します。以降σに斜線が入っているところは置換積分の正しい手順のやり忘れの間違いでした。後で気付いたので、残しておこうと思います。後ほど解説もあります。うっかりうっかりです。知能不足である管理人(自分)の証拠の証拠として残しました。それで計算を進めると $$ \int^{\infty}_{-\infty} \textcolor{red}{(z \cdot \sigma + \mu)^2 } \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$ となって、(3)式の部分を\( (a+b)^2 = a^2+2ab+b^2 \)を適用して、 $$ \int^{\infty}_{-\infty} \textcolor{red}{(z^2 \cdot \sigma^2 + 2z\cdot \sigma \cdot \mu + \mu^2) } \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{\textcolor{blue}{z^{2}}}{2}}\cdot dz $$ となります。(2)式は\( \frac{1}{\sigma^{2}}(x-\mu)^{2} \)を\( z^{2} \)と置き換えてます。そして上記の式を分配法則\( (a + b)x = ax + bx \)のような計算と同じ要領を適用して $$ \int^{\infty}_{-\infty} z^2 \cdot \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz+ \int^{\infty}_{-\infty} 2z\cdot \sigma \cdot \mu \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz + \int^{\infty}_{-\infty} \mu^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}}e^{-\frac{z^{2}}{2}}\cdot dz $$ 定数倍部分を積分の外に出しても問題ないので外に出した表記にしてみます。 $$ \sigma^2 \cdot \int^{\infty}_{-\infty} z^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 2\sigma\mu \cdot \int^{\infty}_{-\infty}z \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz + \mu^2 \cdot \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz $$ 真ん中の項は先の平均値の算出でやったとおり奇関数なので積分をすると0です。一番後ろの項は積分の部分が確率密度関数そのものなので1になります。\( \sqrt{2 \pi}\sigma \)の\( \sigma \)はあっても無くてもゼロでなければグラフでは高さと広がりかたが変化する要素で、zに置換されて指数部の分母にもσがない状態においては、確率密度関数の積分は1になります。で、一番最初の項目がどうなるかを考えないといけないです。まずは整理したものを以下に記述すると $$ \sigma^2 \cdot \int^{\infty}_{-\infty} z^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 2\sigma\mu \cdot 0 + \mu^2 \cdot 1 $$ $$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot \int^{\infty}_{-\infty} z^2 \cdot e^{-\frac{z^{2}}{2}}\cdot dz+ 0 + \mu^2 $$
部分積分の公式を使って
| $$ \int f(x) \cdot g^{\prime}(x) \cdot dx = f(x) \cdot g(x) - \int f^{\prime}(x) \cdot g(x) \cdot dx $$ |
$$ ( \textcolor{red}{e^{- \frac{z^2}{2}}})^{\prime} = \textcolor{blue}{-z \cdot e^{-\frac{z^2}{2}}} $$ なので、 $$ \int^{\infty}_{-\infty} z^2 \cdot e^{-\frac{z^{2}}{2}}\cdot dz = \int^{\infty}_{-\infty} \textcolor{green}{-z} \cdot \textcolor{blue}{(e^{- \frac{z^2}{2}})^{\prime}} \cdot dz $$ ですから、 $$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} - \int^{\infty}_{-\infty} (\textcolor{green}{-z})^{\prime} \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$ となって $$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} - \int^{\infty}_{-\infty} \textcolor{green}{-1} \cdot \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$ 上記の−1を整理して
$$ = \textcolor{green}{-z} \cdot \textcolor{red}{e^{-\frac{z^2}{2}}} + \int^{\infty}_{-\infty} \textcolor{red}{e^{- \frac{z^2}{2}}} \cdot dz $$
$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot (\left[ -z e^{-\frac{z^{2}}{2}} \right]^{\infty}_{-\infty}+ \int^{\infty}_{-\infty} e^{-\frac{z^{2}}{2}} \cdot dz) + 0 + \mu^2 $$ $$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\cancel{\sigma}} \cdot (0 + \sqrt{2\pi}) + 0 + \mu^2 $$ あれ? $$ \sigma^2 + 0 + \mu^2 $$
になるはずでこれに\( \textcolor{red}{ E[\mathrm{X}^2]} \textcolor{black}{- E[\mathrm{X}]^2 =} \textcolor{red}{(\sigma^2+\mu^2)} \textcolor{black}{ - \mu^2 = \sigma^2} \)となる予定だったんすけど \( \sqrt{2\pi}\sigma \)でσが一個、分母に余計に残った。おかしいなと思って他のサイト見てみたら他のサイトではしれっとσが消えてるとこもありました。神戸大学の人の文献のようです。神戸大学の人の文献では自信をもってσが分母から消えているので、計算は合っているのかもしれないが、自分のわからない理論で消えているのは確かだ。わからない。困った。こんなん考えてるの自分らくらいなので、なかなか自分の計算を助けてくれる文献には出会えない。残念だけど、暫く保留だな。所詮は放送大学卒の頭脳ってことだな。解ける人は解いてみて下さい。神戸大学 樋口教授のノート > > >平成24年度後期の講義ノート(notes for 2012 autumn) > > > 確率論1 ( Probability 1 ), 微分積分学2 ( bibun-sekibun-gaku ) > > >11月2日講義ノート の3ページ目から4ページ目にまたがるところが、自分の謎な部分。
しゅん…。
あ。一晩寝て、気付きました。さすが神戸大学の教授。間違ってるわけがないと思って真剣に上記のNoteを読み込んで、気付きました。置換積分をしているんだということを忘れていました。σはそこから出てきて約分されてきえているに違いないと思ったのです。
置換積分の公式は
| $$ x=g(t) $$ とおくと、 $$\int f(x) \cdot dx= \int f(g(t))\frac{dx}{dt}\cdot dt $$ |
公式をきちんと適用すると具体的には、
$$ x = \sigma \cdot z + \mu $$
とおいているので
$$ \frac{dx}{dz} $$
は
$$ \sigma \cdot z + \mu $$
というxの式をzで微分するという意味で、
$$ \frac{dx}{dz} = \sigma $$
になるので、zで置換した積分の式に\( \frac{dx}{dz}\)を掛けるのが置換積分ですから、以下のようになります。
$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}\sigma} \cdot \textcolor{red}{ \sigma } \textcolor{black}{ \cdot \int^{\infty}_{-\infty}-z e^{-\frac{z^{2}}{2}}\cdot dz } $$
なので、
$$ \sigma^2 \cdot \frac{1}{\sqrt{2\pi}} \cdot (\int^{\infty}_{-\infty}-z e^{-\frac{z^{2}}{2}}\cdot dz $$
となります。
だから、σが分母に残っていたのは無くなって
$$ \sigma^2 + 0 + \mu^2 $$
になります。なので、
$$ E[\mathrm{X^2}] = \sigma^2 + 0 + \mu^2 $$
ですから、分散\( V[X] = \textcolor{red}{ E[\mathrm{X^2}] } - \textcolor{blue}{ E[\mathrm{X}]^2 } \)VはVarianceのVで、これは
$$ V[X] = \textcolor{red}{ \sigma^2 + 0 + \mu^2 } \textcolor{black}{-} \textcolor{blue}{\mu^2} $$
$$ V[X] = \sigma^2 $$
となるので、
$$ \sigma^2 = \int (x - \mu)^2 \cdot f(x) \cdot dx $$
であることが確認できたことになります。
で、さらに本題に戻って、確率密度関数を作る方法について考えていたので、それについて確かめていきたいと思います。えらい遠回りしてますけど、もうちょっとっすガンバロ。俺。
分散値を求める式から確率密度関数に平均値変数と分散値変数を含めた積分して1になる係数をもつ式を求める
確率密度関数はこうなんじゃないか?という随分前のところで
$$ \int \sqrt{\frac{\mathstrut \mathrm{N}}{\mathstrut \pi}} e^{-\mathrm{N}(x-\mu)^2} \cdot dx = 1 $$
まで求めてました。積分して1になるちょうど良い膨らみの係数を求めることです。
でも、これって求めるのってガウスさん位の奇才でないと思いつかないことなんです。どうなっていたら都合がいいのか?その数学の魔術師の才能の考え方の一部がここまで説明してきた確率密度関数から平均値を求めることであったり、確率密度関数から分散値を求めることに適しているようなNという係数なのです。どちらかというとネイピア数つまりエクスポーネンシャルeの右上に記述されているNを優先的に決めて、それに対応するものがeの手前のNにも関わってくるということになります。結果的には \( N = \frac{1}{2\sigma^2} \)になります。Nが何であっても、積分の結果が1になるのですから、あとはこの関数が役立つ事を目指します。係数はグラフで言う所のx=0のときのyの値である上凸の最大値と広がりが決まります。
とにかく、何で\( N = \frac{1}{2\sigma^2} \)が都合がいいのかを後は考えれば良いことになります。
まずは分散\( \sigma^2 \)が式の中で影響して、グラフにおいてもなんらかの役割が働かないといけません。なので\( N = \sigma^2 \)にしたらどうなるのか?ということを考えます。
この場合、σが大きくなるほどグラフの広がりが小さくなり頂点の位置が高くなるような感じになってしまいます。データが分散するイメージとは逆になります。なので、逆数の\( \frac{1}{\sigma^2} \)を掛けます。あとは結果的に出てくる\( \frac{1}{2} \)だけがどこからやってきたのか?を考えるだけですが、これがナカナカ凡人の自分にはわからない。\( \frac{1}{2\sigma^2} \)と\( \frac{1}{\sigma^2} \)とで比べると2で割ってる方が広がりが大きめになります。じゃなんで2で割ってる方が使われてるの?ここが、とても重要なポイントで、データの分散値以内になる確率が面積から求められるための調整がされています。さすがにここは感覚的な議論ではなく、計算に基づいて決められていそうです。
さてさて、これってどうやって調べればいいの?と思ったのが自分でして、いろいろインターネットにある正規分布の確率密度の導出に関わる文献をいろいろと調べましたが、明確な答えを見つけ出すことが出来ませんでした。もうちょっと調べてみよかな。
ん~考えてもわからないので、まずは実際の数値がどうなるかを確認してみましょう。
\( \frac{1}{2\sigma^2} \)の場合のσの値毎の面積を確認します。こっちは正しい方の値ですので、よく見かける値でしょう。1σは正規分布におけるx軸の値が-1から1までの積分値(グラフの面積)です。xを-10~10に変動した場合は、10σと表現して、面積はほぼ1になります。これを%表記で100%とすると
1σ = 68.27%、2σ= 95.45%、3σ=99.73%、… 6σ=99.999999808520
となります。6σは間違いの起こりえる世界でも正しいことが起こる確率を極限に高めた状態で100万回に1回くらいの間違いや100万個に1個の不良しかでない状態として有名な値です。6σを達成してこそ世に出せる製品と言えるというのが日本品質みたいなね。過剰品質と呼ばれることもありますが、伝統的なモノとして受け継がれています。悪習とみられて、緩い考えのモノも増えてきてはいます。良品維持コストと不良発生リスクのバランスが大事になります。命に係わるものほど6σを基準にしたモノづくりを目指してほしいです。そして、その100万個に1個さえも失敗や不良として検出できるのが理想なんでしょう。開発段階なんかでは、まずは3σくらいは達成しないとね。ってそんな感じで現場では使われています。
で、\( \frac{1}{\sigma^2} \)だと、どうなるでしょう。
1σ = 84.27%、2σ= 99.53%、3σ=99.9978%、… 6σ=99.999999999998 (※例えばの悪い例なので、コレを参考にしてはダメ。正しいのはもう少し上にあります。)
と間違いの計算をすると、誰かが勘違いしそうで、怖いですが、上記のように1σでもかなりの範囲が収まる(ちょっと離れただけで面積が1に迫る)急峻な凸グラフになってしまいます。前者の方がちょうど良い塩梅であることがわかります。誰がどうやって決めたのか?式の考案者ド・モアブルさんとか、\( \int e^{-x} \cdot dx = \sqrt{\pi} \)と計算したガウス積分の発案者ガウスさんに聞いた方が早いかもしれませんが、自分ではここまでしか迫ることは出来ませんでした。いろいろなサイトをみてもエクスポーネンシャルの乗数\( \frac{1}{2} \)とエクスポーネンシャルの手前に出ている\( \frac{1}{\sqrt{2}} \)が同じになることを証明しているだけで、なんで2が生まれたのかについては触れられていないように感じます。
また、年月を重ねて統計学歴史書なんかに触れることが出来たら、知ることができると思いますので、それまでは、これ以上のことは、そっとしておきましょう。
現代において、100程ある分布関数を前にして
http://www.math.wm.edu/~leemis/chart/UDR/UDR.html
初歩の初歩である正規分布さえも理解しきれていないと感じてしまうと、自分の知識の浅さを思い知らされます。なんなんこれ?というリンク先です。恐るべし統計学。
アンダーラインCSSのサンプル [蛍光ペンを模した形式]
赤色系統
<span style = "background:linear-gradient(transparent 75%, #ffadad 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ff9393 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ff7f7f 75%); font-weight:bold; ">正規分布</span>
正規分布
水色系統
<span style = "background:linear-gradient(transparent 75%, #c1e0ff 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #9eceff 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; ">正規分布</span>
正規分布
黄色系統
<span style = "background:linear-gradient(transparent 75%, #fff799 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #edde7b 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ffdc00 75%); font-weight:bold; ">正規分布</span>
正規分布
緑色系統
<span style = "background:linear-gradient(transparent 75%, #b2ffb2 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #7fff7f 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #bfff7f 75%); font-weight:bold; ">正規分布</span>
正規分布
桃色系統
<span style = "background:linear-gradient(transparent 75%, #ffc1e0 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ffc0cb 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ff9ece 75%); font-weight:bold; ">正規分布</span>
正規分布
淡水色系統
<span style = "background:linear-gradient(transparent 75%, #c1ffff 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #bce2e8 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #afeeee 75%); font-weight:bold; ">正規分布</span>
正規分布
橙色系統
<span style = "background:linear-gradient(transparent 75%, #ffe0c1 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ffce9e 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ffbf7f 75%); font-weight:bold; ">正規分布</span>
正規分布
紫色系統
<span style = "background:linear-gradient(transparent 75%, #cab8d9 75%); font-weight:bold; ">正規分布</span>
正規分布
<span style = "background:linear-gradient(transparent 75%, #ce9eff 75%); font-weight:bold; ">正規分布</span>
正規分布
アニメーションマーカー
蛍光ペンのようなアンダーラインをつけたい文字が画面に表示されてからアニメーションを伴って、左から右にアンダーラインが引かれていくように見せる方法です。HTMLに以下のようなスクリプトを同じファイル内にまとめて記述することで実現出来ます。javascriptとcssと利用部分の3つのセクションから構成されます。同一のファイルにまとめて記載したくない場合はjavascript部分とcss部分を別ファイルにして、HTML内で読み込むようにして利用して下さい。
- 横幅200%に拡大して、linear-gradientで左をアンダーライン右を透明にする方式
javascript
<script>
$(window).scroll(function (){
$(".marker-animation").each(function(){
var position = $(this).offset().top; //ページの一番上から要素までの距離を取得
var scroll = $(window).scrollTop(); //現在表示している画面の上部部分についてページ位置情報を取得
var windowHeight = $(window).height(); //ウインドウの高さを取得
if (scroll > position - windowHeight){ //アニメーションマーカーを行う文字の位置から
//画面の高さを引いた部分よりスクロール位置が大きくなったら
$(this).addClass('active'); //.marker-animationのactiveというスタイル要素状態を設定する
}
});
});
</script>
css
<style type= "text/css">
.marker-animation.active{ /*mraker-animation.activeというスタイルになると*/
background-position: -100% .5em; /*背景200%の大きさの領域の右から100%の部分が左下隅に*/
/*なるように位置に背景領域を設定する。*/
/*更に背景高さ位置を上から0.5em(1emは文字1文字分の幅に相当なので、*/
/*文字半分くらい)に設定、背景領域の下側が押し出される感じ */
}
.marker-animation {
background-image: -webkit-linear-gradient(left, transparent 50%, rgb(255,250,153) 50%);
background-image: -moz-linear-gradient(left, transparent 50%, rgb(255,250,153) 50%);
background-image: -ms-linear-gradient(left, transparent 50%, rgb(255,250,153) 50%);
background-image: -o-linear-gradient(left, transparent 50%, rgb(255,250,153) 50%);
background-image: linear-gradient(to left, transparent 50%, rgb(255,250,153) 50%);
/*全てlinear-gradientだけど上4つはブラウザ毎の設定 */
/*200%の横幅に対して右から半分は透明に残りは指定色に*/
/* ブラウザ毎の分けられたcssの記載はベンダープレフィックス */
/* と呼びます。linear-gradientはcss3の技術で2018年に勧告済み */
/* 新しいブラウザだけ閲覧できればいいのであれば、 */
/* ベンダープレフィックスの定義は不要です。 */
background-repeat: repeat-x; /*100%を超える領域も使うのでその部分はx方向に繰り返す*/
background-size: 200% .8em; /*領域の大きさは横は2倍に 高さマーカー高さ幅は0.8emに*/
background-position: 0 .5em; /*背景の横位置は0に、上は0.5emに。この位置に戻そうとするような動きになる*/
transition: all 2s ease; /*動かす指定で違うところのpositionになっていると2秒かけて最後に指定した*/
/*positionにする。*/
font-weight: bold;
}
</style>
cssスタイル利用部分
<span class="marker-animation">
ここにマーカーをつける文章をいれる
</span>
background-size: 200% 20%
background-position: 0px 100% ← -100% 100%
ここにマーカーをつける文章をいれる
background-size: 200% 0.8em
background-position: 0px 0.5em ← -100% 0.5em
ここにマーカーをつける文章をいれる
background-size: 200% 0.1em
background-position: 0px 0.5em ← -100% 0.5em
ここにマーカーをつける文章をいれる
- マーカーを縦にグラデーションする方式のスクリプト
javascript
<script>
$(window).scroll(function (){
$(".marker-animation").each(function(){
var position = $(this).offset().top; //ページの一番上から要素までの距離を取得
var scroll = $(window).scrollTop(); //現在表示している画面の上部部分についてページ位置情報を取得
var windowHeight = $(window).height(); //ウインドウの高さを取得
if (scroll > position - windowHeight){ //アニメーションマーカーを行う文字の位置から
//画面の高さを引いた部分よりスクロール位置が大きくなったら
$(this).addClass('active'); //.marker-animationのactiveというスタイル要素状態を設定する
}
});
});
</script>
css
<style type= "text/css">
.marker-animation.active{
background-size: 100% 100%;
background-position: 0px 100%;
}
.marker-animation {
background-image: -webkit-linear-gradient(bottom, transparent 50%, #7fbfff 50%);
background-image: -moz-linear-gradient(bottom, transparent 50%, #7fbfff 50%);
background-image: -ms-linear-gradient(bottom, transparent 50%, #7fbfff 50%);
background-image: -o-linear-gradient(bottom, transparent 50%, #7fbfff 50%);
background-image: linear-gradient(to bottom, transparent 50%, #7fbfff 50%);
background-repeat: no-repeat;
background-size: 0% 100%;
background-position: 0px 100%;
transition: all 5s ease;
font-weight: bold;
}
</style>
lineargradient(to bottom,… -webkit-llineargradient(bottom その他のブラウザ向けもwebkitと同じ
background-repeat: no-repeat:
background-size: 100% 100%; ← 0% 100%;
background-position: 0 100%; ← 0% 100%;
ここにマーカーをつける文章をいれる
縦のグラデーションを活用する例
background-image: linear-gradient(to bottom, transparent 45%, #ff7f7f 77% 90%, #ff9f9f 95%);
ここにマーカーをつける文章をいれる
縦横に透明になるグラデーションがかかったアンダーラインを作るには背景画像を別で準備して、その画像サイズをアニメーションさせるしかないでしょう。そのような縦横に透明をうまくかけるには不透明マスク機能とグループ化やクリップ機能をもったラスタ(ペイント)系あるいはベクター(ドロー)系画像編集アプリケーションが必要になるでしょう。
Sass[Syntactically Awesome StyleSheet]
アニメーションマーカーのような規模のcssになるとちょっとした色変更だけでも大変な量の修正が必要になってきます。そこで考えられたのがcssをプログラムのような記述から自動的に吐き出す方式です。それがSassです。色や各種の値を変数化したり、要素複数を関数のように一纏めにして引数を与えるような構造が利用できるものをSassと呼び、cssによるデザインを繰り返し扱う人には重要なシステムとなっています。SassはコンパイラのようにPCに環境を構築する必要があります。ウェブサービスとして、左ViewにSassを記述すると右Viewに対応するcssを書き出してくれるsassmeisterというsiteがありますが関数のような利用の@mixin構文が動かないという重要な機能の不足やiOSのブラウザでは文字の位置が見た目の位置とカーソルの位置がずれてどの文字部分を編集しようとしているかわからないという欠点があったので使うのをやめました。自分だけの問題かも知れませんが、使いたい人は使ってみると良いでしょう。環境の構築方法はここではあまり説明しませんが、ここでSassの基本について触れたいと思います。
Sassには、css表記方法を簡略化し、括弧やセミコロンの記述が不要なsass表記方法と、 cssの記述方法と似ている scss(正式名称は分かりません)という表記方法があります。自分は従来の記述方式を踏襲しているscss方式のSassを使います。いざと言う時にSassの一部からコピペするだけでcssとして利用できるのは便利です。Sassからcssにするのにはコンパイルや変換が必要で、ワンクッション置かなければならないことを考えれば再利用や簡単な確認を素早く行うには同じ表記方法になっている方が良いと考えるからです。
Pythonの記事へ戻る