AP過去問 令和5年度秋期 午前 問17

AP過去問 令和5年度秋期 午前 問題に戻る

AP過去問 令和5年度秋期 午前 問16前の問題へ

AP過去問 令和5年度秋期 午前 問18次の問題へ

　

問17(問題文)

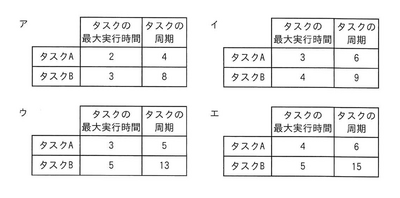
　プリエンプティブな優先度ベースのスケジューリングで実行する二つの周期タスクA及びBがある。タスクBが周期内に処理を完了できるタスクA及びBの最大実行時間及び周期の組合せはどれか。ここで、タスクAの方がタスクBより優先度が高く、かつ、タスクAとBの共有資源はなく、タスク切替え時間は考慮しないものとする。また、時間及び周期の単位はミリ秒とする。

　

回答・解説

【解き方】 タスクBが処理を完了できるかどうかは、応答時間解析(response time analysis)で判断します。

応答時間の式（初期値はタスクBの実行時間から開始）：

$$\require{enclose} \begin{eqnarray} R = C_B + \sum_{i \in hp(B)} \left\lceil \frac{R}{T_i} \right\rceil \cdot C_i \end{eqnarray}$$

​ $C_B$ ：タスクBの最大実行時間

$T_i$：タスクAの周期

$C_i$ ：タスクAの最大実行時間

$\left\lceil \frac{R}{T_i} \right\rceil$は天井関数と呼ばれ、シーリング Ti ぶんの Rのように読みます。これは0.8や0.2のような少数を切り上げ、1とする演算です。タスクBより優先度が高いもの(higher priority B)について総和をとることを意味します。この問題ではタスクBに対してはタスクAの1つしかないので総和をとる必要はありません。

ア：

• タスクA：$C_i=2$、$T_i=4$

• タスクB：$C_B=3$、$T_B=8$

初期値：$R$には仮に$C_B$を入れ、算出された値を次の$R$とします。収束するか、$T_B$を超えるまで計算します。超えるとタスクが滞りますので、駄目です。$T_B$の周期を超えると、次々とBのタスクがやってきて、消化できずに処理が滞ります。

$R=3+\left\lceil \frac{3}{4} \right\rceil \cdot 2=3+1\cdot2=5$

次：

$R=3+\left\lceil \frac{5}{4} \right\rceil \cdot 2=3+2\cdot2=7$

次：

$R=3+\left\lceil \frac{7}{4} \right\rceil \cdot 2=3+2\cdot2=7$(収束)

$→ R=7 \leqq T_B=8$　→ OK、もう答えは定まったのでこれ以上計算する必要はないですね。

でも、念のため、練習を兼ねて、他の選択肢についても計算をしてみましょう。

イ： タスクA：C=3, T=6

タスクB：C=4, T=9

初期： 𝑅=4+⌈46⌉⋅3=4+1⋅3=7 R=4+⌈ 64 ⌉⋅3=4+1⋅3=7

次： 𝑅=4+⌈76⌉⋅3=4+2⋅3=10 R=4+⌈ 67 ⌉⋅3=4+2⋅3=10

次： 𝑅=4+⌈106⌉⋅3=4+2⋅3=10 R=4+⌈ 610 ⌉⋅3=4+2⋅3=10（収束）

→ 𝑅=10>𝑇𝐵=9R=10>T B =9 → NG

ウ： タスクA：C=3, T=5

タスクB：C=5, T=13

初期： 𝑅=5+⌈55⌉･3=5+1⋅3=8 R=5+⌈ 55​ ⌉⋅3=5+1⋅3=8

次： 𝑅=5+⌈85⌉⋅3=5+2⋅3=11 R=5+⌈ 58​ ⌉⋅3=5+2⋅3=11

次： 𝑅=5+⌈115⌉⋅3=5+3⋅3=14 R=5+⌈ 511​ ⌉⋅3=5+3⋅3=14

→ 𝑅=14>𝑇𝐵=13R=14>T B =13 → NG

エ： タスクA：C=4, T=6

タスクB：C=5, T=15

初期： 𝑅=5+⌈56⌉⋅4=5+1⋅4=9 R=5+⌈ 65 ⌉⋅4=5+1⋅4=9

次： 𝑅=5+⌈96⌉⋅4=5+2⋅4=13 R=5+⌈ 69 ⌉⋅4=5+2⋅4=13

次： 𝑅=5+⌈136⌉⋅4=5+3⋅4=17 R=5+⌈ 613 ⌉⋅4=5+3⋅4=17

→ 𝑅=17>𝑇𝐵=15R=17>T B =15 → NG

　

AP過去問 令和5年度秋期 午前 問16前の問題へ

AP過去問 令和5年度秋期 午前 問18次の問題へ

AP過去問 令和5年度秋期 午前 問題に戻る