「AP過去問 令和6年度春期 午前 問77」の版間の差分
(→回答・解説) |
|||
| (同じ利用者による、間の8版が非表示) | |||
| 1行目: | 1行目: | ||
<freescript></script><script type="text/x-mathjax-config"> | |||
MathJax.Ajax.config.path["Contrib"]="https://wiki.yo-net.jp/mathjax/"; | |||
MathJax.Hub.Register.StartupHook("TeX Jax Ready",function (){ | |||
MathJax.Hub.Insert( | |||
MathJax.InputJax.TeX.Definitions.macros,{ | |||
cancel: ["Extension","cancel"], | |||
bcancel: ["Extension","cancel"], | |||
xcancel: ["Extension","cancel"], | |||
cancelto: ["Extension","cancel"] | |||
} | |||
); | |||
}); | |||
MathJax.Hub.Config({ | |||
tex2jax:{ | |||
displayMath: [['$$', '$$'],['\\[', '\\]']], //displayスタイル数式に利用する記号の指定 | |||
inlineMath: [['\\@', '\\@'],['\\(', '\\)']],//inlineスタイル数式に利用する記号の指定 | |||
//ここは使う人が自由に設定する部分です。 | |||
processEscapes: true | |||
}, | |||
TeX:{ | |||
// equationNumbers:{autoNumber: "AMS"}, | |||
extensions: ["[Contrib]/physics/physics.js","[Contrib]/siunitx/siunitx.js", "color.js", "cancel.js"] | |||
}, | |||
"HTML-CSS": { | |||
availableFonts: [], | |||
preferredFont: null, | |||
webFont: "Neo-Euler" | |||
}, | |||
}); | |||
</script> | |||
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.9/MathJax.js?config=TeX-AMS_HTML-full"></script> | |||
<script></freescript> | |||
<freescript></script> | |||
<style> | |||
.table-container { | |||
display: inline-block; | |||
text-align: left; | |||
margin: 20px; | |||
} | |||
.table-header { | |||
display: flex; | |||
justify-content: space-between; | |||
margin-bottom: 5px; | |||
} | |||
</style> | |||
<style> | |||
div.imadake-left mjx-container[jax="CHTML"][display="true"]{text-align: left;} | |||
.imadake-left .MathJax_Display { | |||
text-align: left !important; | |||
font-size: 0.9rem; | |||
} | |||
</style> | |||
<script></freescript> | |||
[[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | [[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | ||
| 11行目: | 65行目: | ||
<div>< | <div style="position: relative; display: inline-block; width: auto;"><div style="position: absolute; top: 0; right: 0; transform: translateY(-100%);">単位 百万円</div><table border="2" style="border-collapse: collapse;border-style: solid"> | ||
<tr> | <tr> | ||
<td align="center" style="border: none; width: 8em;">売上高</td> | <td align="center" style="border: none; width: 8em;">売上高</td> | ||
| 68行目: | 122行目: | ||
=='''回答・解説'''== | =='''回答・解説'''== | ||
損益分岐点売上高は、固定費を限界利益率で割って求めます。 | |||
まず、限界利益を計算します。 | |||
*売上高: <span style="font-size: 0.9rem;">\( 500\text{[百万円]} \)</span> | |||
*変動費(材料費+外注費): <span style="font-size: 0.9rem;">\(200 + 100 = 300\text{[百万円]} \)</span> | |||
*限界利益: <span style="font-size: 0.9rem;">\(500 - 300 = 200\text{[百万円]} \)</span> | |||
*限界利益率: <span style="font-size: 0.9rem;">\(200 ÷ 500 = 0.4 (40\text{[%]}) \)</span> | |||
次に、固定費の合計を求めます。 | |||
*固定費(製造固定費+販売固定費): <span style="font-size: 0.9rem;">\(100 + 80 = 180\text{[百万円]} \)</span> | |||
したがって、損益分岐点売上高は以下の通りです。 | |||
<span style="font-size: 0.9rem;">\(180 ÷ 0.4 = 450\text{[百万円]} \)</span> | |||
したがって | |||
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; "> | |||
ウ</span> | |||
が答えです。 | |||
[[ファイル:損益分岐点分析.png|400px|thumb|none|損益分岐点分析]] | |||
上記のようなグラフが描けます。 | |||
横軸 Xは売上高 | |||
縦軸 Yは金額 | |||
<span style="color: green;">緑の直線(Revenue)</span>は、売上高の増加に比例して増える金額を示しています。 | |||
<span style="color: red;">赤の直線(Total Costs)</span>は、固定費と変動費の合計として、売上高に応じて増加する総費用を示しています。 | |||
<span style="color: blue;">青の破線(Break-even Point)</span>は、売上高と総費用が等しくなり、利益がゼロとなるポイントを示します。 | |||
<span style="color: orange;">オレンジの点線(Fixed Costs)</span>は、売上高に関係なく発生する固定費の金額を示しています。 | |||
緑で塗られた領域(Contribution Margin)は、売上から変動費を差し引いた部分で、企業が固定費を回収し、利益を生むための原資となる部分です。下側は赤い線と並行で、変動費の傾きをもった直線であり、固定費を差し引いた直線で原点をとおる線です。 | |||
グラフの売上高と金額は1対1の関係ですから傾きは1.00です。 | |||
総費用は売上が1百万円増えるごとに、変動費が0.6百万円増えるということです。 | |||
(材料費200+外注費100=300 → 売上500に対して 300 ÷ 500 = 0.6)つまり、'''変動費÷売上'''は'''総費用の傾き'''を表します。'''売上の傾き'''1と、総費用の傾き0.6の'''差である0.4が限界利益率'''を表しています。 | |||
売上のグラフの式 y=x | |||
総費用のグラフの式 y=((変動費: (材料費: 200) + (外注費: 100))÷売上: 500)*x+(固定費: 180) | |||
という連立方程式を解くという作業の過程がそれぞれの定型の算出方法になっているだけです。総費用の傾きにも名前が付いていて、変動費率と呼んでいます。だから変動比率を求める式は変動比率 = (変動費: 300) ÷ (売上: 500)なのです。計算すると(変動比率:0.6)です。そして、売上のグラフの傾き1と変動比率の傾きの差分をとるというのは連立方程式同士の引き算をしているだけで売上のグラフの式と総費用のグラフの式の差分をとる作業をすることで、限界利益率 * x = 固定費という計算式がでてくるのです。つまり限界利益率 + 変動比率 = 1である仕組みも当たり前のことに思えるのです。限界利益=売上-変動費のことで、500-300で200となりますが、限界利益率の傾きを直接求める方法の一つとなっているだけです。(限界利益: 200)÷(売上: 500) = (限界利益率: 0.4)。連立方程式を解く過程のそれぞれの値に名前がついていると考えると良いでしょう。 | |||
総費用の傾きは変動費で割り出せるし、Y軸切片が固定費なのだと覚えておけば、この連立方程式が立てれるし、損益分岐点を求めることができるでしょう。式を覚えるよりは、計算過程の中で出てくる値のそれぞれに名前が付いていると覚える方がいいと思います。そうするとそれぞれの値が大きくなったり小さくなったりしたときの影響もわかるし、それぞれの名前がついている値の意味も捉えやすくなります。 | |||
0.4x=180によって損益分岐点の売上を求めることができる450という答えが算出できるのです。 | |||
2025年4月15日 (火) 19:12時点における最新版
AP過去問 令和6年度春期 午前 問76前の問題へ
AP過去問 令和6年度春期 午前 問78次の問題へ
問77(問題文)
損益計算資料から求められる損益分岐点売上高は、何百万円か。
| 売上高 | 500 | ||
| 材料費(変動費) | 200 | ||
| 外注費(変動費) | 100 | ||
| 製造固定費 | 100 | ||
| 総利益 | 100 | ||
| 販売固定費 | 80 | ||
| 利益 | 20 |
ア 225
イ 300
ウ 450
エ 480
回答・解説
損益分岐点売上高は、固定費を限界利益率で割って求めます。
まず、限界利益を計算します。
- 売上高: \( 500\text{[百万円]} \)
- 変動費(材料費+外注費): \(200 + 100 = 300\text{[百万円]} \)
- 限界利益: \(500 - 300 = 200\text{[百万円]} \)
- 限界利益率: \(200 ÷ 500 = 0.4 (40\text{[%]}) \)
次に、固定費の合計を求めます。
- 固定費(製造固定費+販売固定費): \(100 + 80 = 180\text{[百万円]} \)
したがって、損益分岐点売上高は以下の通りです。
\(180 ÷ 0.4 = 450\text{[百万円]} \)
したがって
ウ
が答えです。
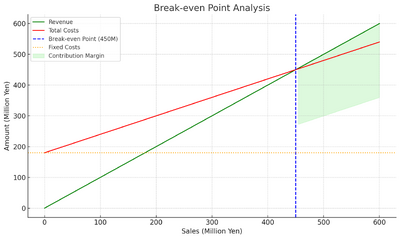
上記のようなグラフが描けます。
横軸 Xは売上高
縦軸 Yは金額
緑の直線(Revenue)は、売上高の増加に比例して増える金額を示しています。
赤の直線(Total Costs)は、固定費と変動費の合計として、売上高に応じて増加する総費用を示しています。
青の破線(Break-even Point)は、売上高と総費用が等しくなり、利益がゼロとなるポイントを示します。
オレンジの点線(Fixed Costs)は、売上高に関係なく発生する固定費の金額を示しています。
緑で塗られた領域(Contribution Margin)は、売上から変動費を差し引いた部分で、企業が固定費を回収し、利益を生むための原資となる部分です。下側は赤い線と並行で、変動費の傾きをもった直線であり、固定費を差し引いた直線で原点をとおる線です。
グラフの売上高と金額は1対1の関係ですから傾きは1.00です。
総費用は売上が1百万円増えるごとに、変動費が0.6百万円増えるということです。
(材料費200+外注費100=300 → 売上500に対して 300 ÷ 500 = 0.6)つまり、変動費÷売上は総費用の傾きを表します。売上の傾き1と、総費用の傾き0.6の差である0.4が限界利益率を表しています。
売上のグラフの式 y=x
総費用のグラフの式 y=((変動費: (材料費: 200) + (外注費: 100))÷売上: 500)*x+(固定費: 180)
という連立方程式を解くという作業の過程がそれぞれの定型の算出方法になっているだけです。総費用の傾きにも名前が付いていて、変動費率と呼んでいます。だから変動比率を求める式は変動比率 = (変動費: 300) ÷ (売上: 500)なのです。計算すると(変動比率:0.6)です。そして、売上のグラフの傾き1と変動比率の傾きの差分をとるというのは連立方程式同士の引き算をしているだけで売上のグラフの式と総費用のグラフの式の差分をとる作業をすることで、限界利益率 * x = 固定費という計算式がでてくるのです。つまり限界利益率 + 変動比率 = 1である仕組みも当たり前のことに思えるのです。限界利益=売上-変動費のことで、500-300で200となりますが、限界利益率の傾きを直接求める方法の一つとなっているだけです。(限界利益: 200)÷(売上: 500) = (限界利益率: 0.4)。連立方程式を解く過程のそれぞれの値に名前がついていると考えると良いでしょう。
総費用の傾きは変動費で割り出せるし、Y軸切片が固定費なのだと覚えておけば、この連立方程式が立てれるし、損益分岐点を求めることができるでしょう。式を覚えるよりは、計算過程の中で出てくる値のそれぞれに名前が付いていると覚える方がいいと思います。そうするとそれぞれの値が大きくなったり小さくなったりしたときの影響もわかるし、それぞれの名前がついている値の意味も捉えやすくなります。
0.4x=180によって損益分岐点の売上を求めることができる450という答えが算出できるのです。
AP過去問 令和6年度春期 午前 問76前の問題へ
AP過去問 令和6年度春期 午前 問78次の問題へ