「AP過去問 令和6年度春期 午前 問52」の版間の差分
(ページの作成:「AP過去問 令和6年度春期 午前 問題に戻る AP過去問 令和6年度春期 午前 問51へ AP過去問 令和6年度春期 午前 問53へ =='''問52(問題文)'''== =='''回答・解説'''== AP過去問 令和6年度春期 午前 問51へ AP過去問 令和6年度春期 午前 問53へ AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午…」) |
編集の要約なし |
||
| (同じ利用者による、間の4版が非表示) | |||
| 1行目: | 1行目: | ||
[[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | [[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | ||
[[AP過去問 令和6年度春期 午前 問51]] | [[AP過去問 令和6年度春期 午前 問51]]前の問題へ | ||
[[AP過去問 令和6年度春期 午前 問53]] | [[AP過去問 令和6年度春期 午前 問53]]次の問題へ | ||
=='''問52(問題文)'''== | =='''問52(問題文)'''== | ||
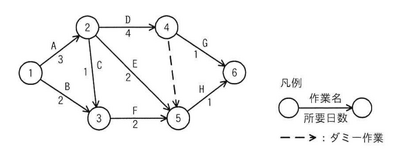
図のアローダイアグラムで表されるプロジェクトがある。結合点5の最早結合点時刻はプロジェクト開始から第何日か。ここで、プロジェクトの開始日は0日目とする。 | |||
[[ファイル:AP R6 1Spring AMQ52 Fig1.png|400px|thumb|none|]] | |||
ア 4 | |||
イ 5 | |||
ウ 6 | |||
エ 7 | |||
=='''回答・解説'''== | =='''回答・解説'''== | ||
この問題では、結合点5の最早結合点時刻を求めます。最早結合点時刻とは、前段の作業がすべて完了して、次の作業に進むことができる最も早い時刻のことです。 | |||
図をもとにして、結合点1(開始点、時刻0)から順に最早時刻を計算していきます。 | |||
5への経路は以下の3とおりが考えられます。 | |||
1→2→4→5 | |||
1→2→5 | |||
1→3→5 | |||
各結合点の最早時刻 | |||
結合点1:0日 | |||
結合点2:0 + A(3) = 3日 | |||
結合点3:0 + B(2) = 2日 | |||
結合点4: | |||
2→4:A(3) + D(4) = 7日 | |||
結合点5: | |||
2→5:A(3) + C(1) = 4日 | |||
3→5:B(2) + F(2) = 4日 | |||
4→5(ダミー):(A(3) + D(4) =) 7 + ダミー(0) = 7日 | |||
⇒ 最大値:7日 | |||
問題は「結合点5の最早結合点時刻」を聞いており、結論では7日です。 | |||
4→5のダミー作業は依存関係を示すだけで、所要日数は0日です。しかし、このダミーを通じて到達できるようになるのは4の完了後であるため、'''結合点4の最早時刻(7日)'''がそのまま結合点5に伝播します。 | |||
一方、他の経路からも結合点5に到達できますが、'''4→5が最も遅い(=最早時刻として有効な経路)'''になります。したがって、結合点5の最早結合点時刻は7日となります。 | |||
したがって | |||
<span style = "background:linear-gradient(transparent 75%, #7fbfff 75%); font-weight:bold; "> | |||
エ</span> | |||
が答えです。 | |||
[[AP過去問 令和6年度春期 午前 問53]] | [[AP過去問 令和6年度春期 午前 問51]]前の問題へ | ||
[[AP過去問 令和6年度春期 午前 問53]]次の問題へ | |||
[[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | [[AP過去問 令和6年度春期 午前#問題|AP過去問 令和6年度春期 午前 問題]]に戻る | ||
2025年4月13日 (日) 22:28時点における最新版
AP過去問 令和6年度春期 午前 問51前の問題へ
AP過去問 令和6年度春期 午前 問53次の問題へ
問52(問題文)
図のアローダイアグラムで表されるプロジェクトがある。結合点5の最早結合点時刻はプロジェクト開始から第何日か。ここで、プロジェクトの開始日は0日目とする。
ア 4
イ 5
ウ 6
エ 7
回答・解説
この問題では、結合点5の最早結合点時刻を求めます。最早結合点時刻とは、前段の作業がすべて完了して、次の作業に進むことができる最も早い時刻のことです。
図をもとにして、結合点1(開始点、時刻0)から順に最早時刻を計算していきます。
5への経路は以下の3とおりが考えられます。 1→2→4→5
1→2→5
1→3→5
各結合点の最早時刻
結合点1:0日
結合点2:0 + A(3) = 3日
結合点3:0 + B(2) = 2日
結合点4:
2→4:A(3) + D(4) = 7日
結合点5:
2→5:A(3) + C(1) = 4日
3→5:B(2) + F(2) = 4日
4→5(ダミー):(A(3) + D(4) =) 7 + ダミー(0) = 7日
⇒ 最大値:7日
問題は「結合点5の最早結合点時刻」を聞いており、結論では7日です。
4→5のダミー作業は依存関係を示すだけで、所要日数は0日です。しかし、このダミーを通じて到達できるようになるのは4の完了後であるため、結合点4の最早時刻(7日)がそのまま結合点5に伝播します。
一方、他の経路からも結合点5に到達できますが、4→5が最も遅い(=最早時刻として有効な経路)になります。したがって、結合点5の最早結合点時刻は7日となります。
したがって
エ
が答えです。
AP過去問 令和6年度春期 午前 問51前の問題へ
AP過去問 令和6年度春期 午前 問53次の問題へ